Lauren Ipsum: A Story About Computer Science and Other Improbable Things (17 page)

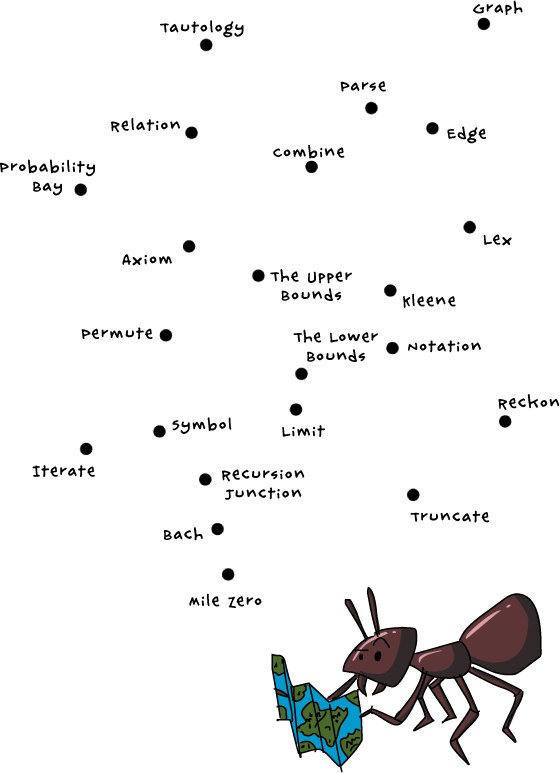
If there are millions of possible ways to solve a difficult problem, searching for the best
solution just isn’t practical. When that happens, scientists use
heuristics
to find an answer that is, as Hugh Rustic might say, “good
enough.”

Heuristic algorithms are based on experience—on things that we know will work—but
they aren’t guaranteed to be the best possible solutions. For example, Hugh Rustic’s
ants find many different paths on the map at random, and by following the scent trails of other
ants. Scent trails eventually dry up if no new ants follow them. The shorter a path is, the more
ants follow it, which makes the scent stronger. Over time, shorter paths become more popular and
longer ones fade away. Based on what Laurie saw the ants do, she knows the path is short, even if it
may not be the shortest, so she can use that as a heuristic to get home more quickly.

Something to think about: Is Hugh Rustic’s ant map through Userland the shortest
possible path, or is it only a short-enough path? Can you do better? Try it!

Much as Xor said, an
axiom
is a rule or principle that you can’t
prove, but that everyone accepts as true because it just makes sense. Mathematicians, scientists,
and anyone who wants to prove anything might start their argument with an axiom.

For example, the idea that
part
of a thing is always smaller than the
entire
thing is an axiom. If you cut a slice out of a pie, there’s no way
that slice can be bigger than the whole pie. The same rule applies to numbers: if you take 2 away
from 5, you’re left holding a 2 and a 3, and neither is more than 5.

Jane Hecate checks each letter of Laurie’s password guesses one by one until there is a
mismatch with the correct password. The more letters Laurie gets correct in a row, the longer it
takes for Jane to find a mismatch, which tells Laurie how close her guess is to being right.

Computer scientists call this a
timing attack
because the guesser watches
the amount of time it takes to check each incorrect try and makes new guesses based on that. Many
people who should know better make Jane’s mistake and leak information about the secret they
are keeping.

As Trent Escrow explains to Laurie, you can guarantee a fifty-fifty chance of flipping heads
or tails on an unbalanced coin—if you flip it twice. If you get Heads-Tails, then Heads is
your answer. If you get Tails-Heads, then Tails is your answer. At least half of the time,
you’ll probably flip Heads-Heads or Tails-Tails; in those cases, just start over. On average,
you’ll need at least three coin flips to get a Fair flip. Try it! See also
Fair
Coin
(
Chapter 6
;
Hamiltonian Cycle
).

. . . is not actually a crime in any jurisdiction, and that’s a good thing! Otherwise,
no one would be allowed to write any stories, and
myths
are just stories that
have been passed down to us through many generations. Some myths try to explain how the world works,
and some are just for fun. Use your imagination, and maybe someday, you’ll write a story that
becomes part of a future mythology.

The
Doppelganger
’s tale is based on a classic question in
philosophy: If you replace all of the parts of a boat, do you still have the same boat? Winsome
doesn’t think so. She claims she stole the
Doppelganger
from its owner
piece by piece and left him with a copy! But what do you think? If you reassemble the old parts,
which boat is the original? What if you replaced only half of the parts?

Conway’s Game of Life
is a simulation of how a population of
creatures might change over time. Computer scientists (and plenty of other scientists) use the Game
of Life to study patterns based on simple rules. You can try it out yourself with a pencil and
paper! First, grab some graph paper or draw a grid like this:

Now fill in some squares in the grid. Here’s one example:

After you’ve filled in some squares, you just have to follow a few simple rules to play
the game and change your pattern:

Follow these rules to color in a new grid. Our sample grid would turn out like this after one
round:

These patterns come in many types.
Gliders
move around.
Blinkers
turn on and off, like traffic lights. Some patterns even create other
patterns as they go. This particular grid pattern repeats:

When scientists want to get to the root cause of a confusing problem, they’ll ask Why
questions until they find out exactly Where their experiment went Wrong. But you don’t have to
leave that kind of thinking to the scientists.

Play Five Whys the next time you need to figure out the solution to a problem of your own.
There are a lot of mental games you can try to help you avoid or learn from mistakes. Another good
rule is “Never worry alone.” Grab a friend if you’re puzzled—when you work
together, you can solve any problem!

The word
Byzantine
can describe any extremely long and complicated
process. Fortunately, Laurie was able to get all of the signatures she needed by helping the three
generals, and she actually solved each of their very different problems similarly.

Laurie’s algorithm for moving the wolf, the goat, and the mandelbroccoli uses a
counting argument
. The idea behind a counting argument is that you can solve
some problems by ignoring unimportant differences between things and counting only how many there
are. For example:

Sometimes it’s the opposite: you have to count the same thing different ways to see if
they add up. General Case stopped counting posts after he hit 100 feet of fence; he wasn’t
thinking about holding up the last length! Count the gaps
between
the posts and
you get 10. Count the
posts
, and you get 11.

When Tinker tells Laurie to count paths that are mirror images of other paths (like BCD and
DCB) as one, he is also using a counting argument. This rule cuts the number of paths through
Userland in half. But even cutting the number in half doesn’t help much with the Traveling
Salesman problem: a Very Big Number divided by a small number is still a Very Big Number!

Mandelbroccoli does exist in our world, and it’s the weirdest-looking vegetable I know.
At the market, it’s called
Romanesco
, and it looks a lot like a fractal.
Fractals
are patterns that start with one shape and repeat it infinitely,
smaller and smaller, according to a set of rules.

For example, draw an equilateral triangle (a triangle with three sides that are all the same
length) inside another equilateral triangle. Make sure each point from the second triangle touches
the middle of a side from the first! This should create four smaller, but identical, triangles
inside the original.

Now, draw an equilateral triangle inside each of those, following the same rules, and repeat
until you can’t fit any more triangles. You should have something like the fractal pattern
shown here. See also
Infinity
(
Chapter 4
;
Infinity
).

“Sierpinski triangle evolution.” Licensed under public domain
via Wikimedia Commons.