In Pursuit of the Unknown (3 page)

There is tantalising evidence that Pythagoras's theorem was known long before Pythagoras. A Babylonian clay tablet
²
in the British Museum contains, in cuneiform script, a mathematical problem and answer that can be paraphrased as:

4 is the length and 5 the diagonal. What is the breadth?

4 times 4 is 16.

5 times 5 is 25.

Take 16 from 25 to obtain 9.

What times what must I take to get 9?

3 times 3 is 9.

Therefore 3 is the breadth.

So the Babylonians certainly knew about the 3–4–5 triangle, a thousand years before Pythagoras.

Another tablet, YBC 7289 from the Babylonian collection of Yale University, is shown in
Figure 3
(
left
). It shows a diagram of a square of side 30, whose diagonal is marked with two lists of numbers: 1, 24, 51, 10 and 42, 25, 35. The Babylonians employed base-60 notation for numbers, so the first list actually refers to 1 + 24/60 + 51/60
²
+ 10/60
³
, which in decimals is 1.4142129. The square root of 2 is 1.4142135. The second list is 30 times this. So the Babylonians knew that the diagonal of a square is its side multiplied by the square root of 2. Since 1
²
+ 1
²
= 2 = (
)
²
, this too is an instance of Pythagoras's theorem.

Fig 3
Left
: YBC 7289.
right
: Plimpton 322.

Even more remarkable, though more enigmatic, is the tablet Plimpton 322 from George Arthur Plimpton's collection at Columbia University,
Figure 3
(right). It is a table of numbers, with four columns and 15 rows. The final column just lists the row number, from 1 to 15. In 1945 historians of science Otto Neugebauer and Abraham Sachs
³
noticed that in each row, the square of the number (say
c
) in the third column, minus the square of the number (say
b
) in the second column, is itself a square (say
a
). It follows that
a
²
+
b
²
=
c
²
, so the table appears to record Pythagorean triples. At least, this is the case provided four apparent errors are corrected. However, it is not absolutely certain that Plimpton 322 has anything to do with Pythagorean triples, and even if it does, it might just have been a convenient list of triangles whose areas were easy to calculate. These could then be assembled to yield good approximations to other triangles and other shapes, perhaps for land measurement.

Another iconic ancient civilisation is that of Egypt. There is some
evidence that Pythagoras may have visited Egypt as a young man, and some have conjectured that this is where he learned his theorem. The surviving records of Egyptian mathematics offer scant support for this idea, but they are few and specialised. It is often stated, typically in the context of pyramids, that the Egyptians laid out right angles using a 3–4–5 triangle, formed from a length of string with knots at 12 equal intervals, and that archaeologists have found strings of that kind. However, neither claim makes much sense. Such a technique would not be very reliable, because strings can stretch and the knots would have to be very accurately spaced. The precision with which the pyramids at Giza are built is superior to anything that could be achieved with such a string. Far more practical tools, similar to a carpenter's set square, have been found. Egyptologists specialising in ancient Egyptian mathematics know of no records of string being employed to form a 3–4–5 triangle, and no examples of such strings exist. So this story, charming though it may be, is almost certainly a myth.

If Pythagoras could be transplanted into today's world he would notice many differences. In his day, medical knowledge was rudimentary, lighting came from candles and burning torches, and the fastest forms of communication were a messenger on horseback or a lighted beacon on a hilltop. The known world encompassed much of Europe, Asia, and Africa – but not the Americas, Australia, the Arctic, or the Antarctic. Many cultures considered the world to be flat: a circular disc or even a square aligned with the four cardinal points. Despite the discoveries of classical Greece this belief was still widespread in medieval times, in the form of
orbis terrae
maps,
Figure 4
.

Who first realised the world is round? According to Diogenes Laertius, a third-century Greek biographer, it was Pythagoras. In his book
Lives and Opinions of Eminent Philosophers
, a collection of sayings and biographical notes that is one of our main historical sources for the private lives of the philosophers of ancient Greece, he wrote: ‘Pythagoras was the first who called the Earth round, though Theophrastus attributes this to Parmenides and Zeno to Hesiod.' The ancient Greeks often claimed that major discoveries had been made by their famous forebears, irrespective of historical fact, so we can't take the statement at face value, but it is not in dispute that from the fifth century
BC
all reputable Greek philosophers and mathematicians considered the Earth to be round. The idea does seem to have originated around the time of Pythagoras, and it might have come from one of his followers. Or it might have been common currency, based
on evidence such as the round shadow of the Earth on the Moon during an eclipse, or the analogy with an obviously round Moon.

Fig 4
Map of the world made around 1100 by the Moroccan cartographer al-Idrisi for King Roger of Sicily.

Even for the Greeks, though, the Earth was the centre of the universe and everything else revolved around it. Navigation was carried out by dead reckoning: looking at the stars and following the coastline. Pythagoras's equation changed all that. It set humanity on the path to today's understanding of the geography of our planet and its place in the Solar System. It was a vital first step towards the geometric techniques needed for mapmaking, navigation, and surveying. It also provided the key to a vitally important relation between geometry and algebra. This line of development leads from ancient times right through to general relativity and modern cosmology, see
Chapter 13
. Pythagoras's equation opened up entirely new directions for human exploration, both metaphorically and literally. It revealed the shape of our world and its place in the universe.

Many of the triangles encountered in real life are not right-angled, so the equation's direct applications may seem limited. However, any triangle can be cut into two right-angled ones as in
Figure 6
(page 11), and any polygonal shape can be cut into triangles. So right-angled triangles are the key: they prove that there is a useful relation between the shape of a triangle and the lengths of its sides. The subject that developed from this insight is trigonometry: ‘triangle measurement'.

The right-angled triangle is fundamental to trigonometry, and in particular it determines the basic trigonometric functions: sine, cosine, and tangent. The names are Arabic in origin, and the history of these functions and their many predecessors shows the complicated route by which today's version of the topic arose. I'll cut to the chase and explain the eventual outcome. A right-angled triangle has, of course, a right angle, but its other two angles are arbitrary, apart from adding to 90°. Associated with any angle are three functions, that is, rules for calculating an associated number. For the angle marked
A
in
Figure 5
, using the traditional
a
,
b
,
c
for the three sides, we define the sine (sin), cosine (cos), and tangent (tan) like this:

sin
A
=
a
/
c
cos
A
=
b
/
c
tan
A
=
a
/
b

These quantities depend only on the angle
A
, because all right-angled triangles with a given angle
A
are identical except for scale.

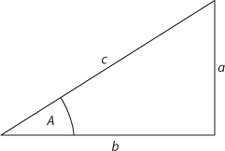
Fig 5
Trigonometry is based on a right-angle triangle.

In consequence, it is possible to draw up a table of the values of sin, cos, and tan, for a range of angles, and then use them to calculate features of right-angled triangles. A typical application, which goes back to ancient times, is to calculate the height of a tall column using only measurements made on the ground. Suppose that, from a distance of 100 metres, the angle to the top of the column is 22°. Take
A
= 22° in
Figure 5
, so that
a
is the height of the column. Then the definition of the tangent function tells us that

tan 22° =
a
/100

so that

a
= 100 tan 22°.

Since tan 22° is 0.404, to three decimal places, we deduce that
a
= 40.4 metres.