Hyperspace (38 page)
Authors: Michio Kaku,Robert O'Keefe

Newton’s theory of gravity, in fact, gives the precise relationship between the escape velocity and the mass of the star. The heavier the planet or star and the smaller its radius, the larger the escape velocity necessary to escape its gravitational pull. As early as 1783, the English astronomer John Michell used this calculation to propose that a super massive star might have an escape velocity equal to the speed of light. The light emitted by such a massive star could never escape, but would orbit around it. Thus, to an outside observer, the star would appear totally black. Using the best knowledge available in the eighteenth century, he actually calculated the mass of such a black hole.
*
Unfortunately, his theory was considered to be crazy and was soon forgotten. Nevertheless, today we tend to believe that black holes exist because our telescopes and instruments have seen white dwarfs and neutron stars in the heavens.
There are two ways to explain why black holes are black. From the
pedestrian point of view, the “force” between the star and a light beam is so great that its path is bent into a circle. Or one can take the Einsteinian point of view, in which case the “shortest distance between two points is a curved line.” Bending a light beam into a full circle means that space itself has been bent full circle. This can happen only if the black hole has completely pinched a piece of space-time along with it, so the light beam is circulating in a hypersphere. This piece of space-time has now disconnected itself from the space-time around it. Space itself has now “ripped.”
The relativistic description of the black hole comes from the work of Karl Schwarzschild. In 1916, barely a few months after Einstein wrote down his celebrated equations, Schwarzschild was able to solve Einstein’s equations exactly and calculate the gravitational field of a massive, stationary star.
Schwarzschild’s solution has several interesting features. First, a “point of no return” surrounds the black hole. Any object that comes closer than this radius will inevitably be sucked into the black hole, with no possibility of escape. Inexorably, any person unfortunate enough to come within the Schwarzschild radius would be captured by the black hole and crushed to death. Today, this distance from the black hole is called the
Schwarzschild radius
, or the
horizon
(the farthest visible point).
Second, anyone who fell within the Schwarzschild radius would be aware of a “mirror universe” on the “other side” of space-time (
Figure 10.2
). Einstein was not worried about the existence of this bizarre mirror universe because communication with it was impossible. Any space probe sent into the center of a black hole would encounter infinite curvature; that is, the gravitational field would be infinite, and any material object would be crushed. The electrons would be ripped off atoms, and even the protons and neutrons within the nuclei themselves would be torn apart. Also, to penetrate through to the alternative universe, the probe would have to go faster than the speed of light, which is not possible. Thus although this mirror universe is mathematically necessary to make sense of the Schwarzschild solution, it could never be observed physically.
Consequently, the celebrated
Einstein-Rosen bridge
connecting these two universes (named after Einstein and his collaborator, Nathan Rosen) was considered a mathematical quirk. The bridge was necessary
to have a mathematically consistent theory of the black hole, but it was impossible to reach the mirror universe by traveling through the Einstein-Rosen bridge. Einstein-Rosen bridges were soon found in other solutions of the gravitational equations, such as the Reissner-Nordstrom solution describing an electrically charged black hole. However, the Einstein-Rosen
bridge remained a curious but forgotten footnote in the lore of relativity.
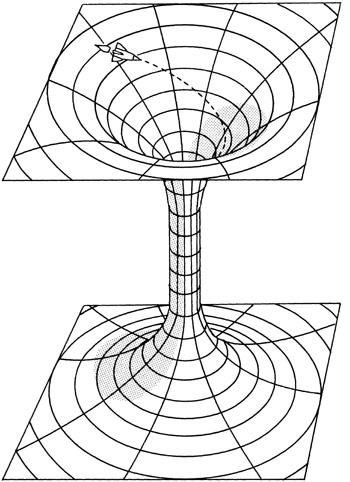
Figure 10.2. The Einstein-Rosen bridge connects two different universes. Einstein believed that any rocket that entered the bridge would be crushed, thereby making communication between these two universes impossible. However, more recent calculations show that travel through the bridge might be very difficult, but perhaps possible
.
Things began to change with the work of New Zealand mathematician Roy Kerr, who in 1963 found another exact solution to Einstein’s equations. Kerr assumed that any collapsing star would be rotating. Like a spinning skater who speeds up when bringing in his or her hands, a rotating star would necessarily accelerate as it began to collapse. Thus the stationary Schwarzschild solution for a black hole was not the most physically relevant solution of Einstein’s equations.
Kerr’s solution created a sensation in the field of relativity when it was proposed. Astrophysicist Subrahmanyan Chandrasekhar once said,
In my entire scientific life, extending over forty-five years, the most shattering experience has been the realization that an exact solution of Einstein’s equations of general relativity, discovered by the New Zealand mathematician Roy Kerr, provides the
absolutely exact representation
of untold numbers of massive black holes that populate the universe. This “shuddering before the beautiful,” this incredible fact that a discovery motivated by a search after the beautiful in mathematics should find its exact replica in Nature, persuades me to say that beauty is that to which the human mind responds at its deepest and most profound level.’
3
Kerr found, however, that a massive rotating star does not collapse into a point. Instead, the spinning star flattens until it eventually is compressed into a ring, which has interesting properties. If a probe were shot into the black hole from the side, it would hit the ring and be totally demolished. The curvature of space-time is still infinite when approaching the ring from the side. There is still a “ring of death,” so to speak, surrounding the center. However, if a space probe were shot into the ring from the top or bottom, it would experience a large but finite curvature; that is, the gravitational force would not be infinite.
This rather surprising conclusion from Kerr’s solution means that any space probe shot through a spinning black hole along its axis of rotation might, in principle, survive the enormous but finite gravitational fields at the center, and go right on through to the mirror universe without being destroyed by infinite curvature. The Einstein-Rosen bridge acts like a tunnel connecting two regions of space-time; it is a wormhole. Thus the Kerr black hole is a gateway to another universe.
Now imagine that your rocket has entered the Einstein-Rosen bridge. As your rocket approaches the spinning black hole, it sees a
ring-shaped spinning star. At first, it appears that the rocket is headed for a disastrous crash landing as it descends toward the black hole from the north pole. However, as we get closer to the ring, light from the mirror universe reaches our sensors. Since all electromagnetic radiation, including radar, orbits the black hole, our radar screens are detecting signals that have been circulating around the black hole a number of times. This effect resembles a hall of mirrors, in which we are fooled by the multiple images that surround us. Light goes ricocheting across numerous mirrors, creating the illusion that there are numerous copies of ourselves in the hall.
The same effect occurs as we pass through the Kerr black hole. Because the same light beam orbits the black hole numerous times, our rocket’s radar detects images that have gone spinning around the black hole, creating the illusion of objects that aren’t really there.
Does this mean that black holes can be used for travel throughout the galaxy, as in
Star Trek
and other science-fiction movies?
As we saw earlier, the curvature in a certain space is determined by the amount of matter-energy contained in that space (Mach’s principle). Einstein’s famous equation gives us the precise degree of space-time bending caused by the presence of matter-energy.
When Captain Kirk takes us soaring through hyperspace at “warp factor 5,” the “dilithium crystals” that power the
Enterprise
must perform miraculous feats of warping space and time. This means that the dilithium crystals have the magical power of bending the space-time continuum into pretzels; that is, they are tremendous storehouses of matter and energy.
If the
Enterprise
travels from the earth to the nearest star, it does not physically move to Alpha Centauri—rather, Alpha Centauri comes to the
Enterprise
. Imagine sitting on a rug and lassoing a table several feet away. If we are strong enough and the floor is slick enough, we can pull the lasso until the carpet begins to fold underneath us. If we pull hard enough, the table comes to us, and the “distance” between the table and us disappears into a mass of crumpled carpeting. Then we simply hop across this “carpet warp.” In other words, we have hardly moved; the space between us and the table has contracted, and we just step across this contracted distance. Similarly, the
Enterprise
does not really cross the entire space to Alpha Centauri; it simply moves across the crumpled
space-time—through a wormhole. To better understand what happens when one falls down the Einstein-Rosen bridge, let us now discuss the topology of wormholes.
To visualize these multiply connected spaces, imagine that we are strolling down New York’s Fifth Avenue one bright afternoon, minding our own business, when a strange floating window opens up in front of us, much like Alice’s looking glass. (Never mind for the moment that the energy necessary to open this window might be enough to shatter the earth. This is a purely hypothetical example.)
We step up to the hovering window to take a closer look, and are horrified to find ourselves staring at the head of a nasty-looking
Tyrannosaurus rex
. We are about to run for our lives, when we notice that the tyrannosaur has no body. He can’t hurt us because his entire body is clearly on the other side of the window. When we look below the window to find the dinosaur’s body, we can see all the way down the street, as though the dinosaur and the window weren’t there at all. Puzzled, we slowly circle the window and are relieved to find that the tyrannosaur is nowhere to be found. However, when we peer into the window from the back side, we see the head of a brontosaur staring us in the face (
Figure 10.3
)!
Frightened, we walk around the window once more, staring at the window sideways. Much to our surprise, all traces of the window, the tyrannosaur, and the brontosaur are gone. We now take a few more turns around the floating window. From one direction, we see the head of the tyrannosaur. From the other direction, we see the head of the brontosaur. And when we look from the side, we find that both the mirror and the dinosaurs have disappeared.
What’s happening?
In some faraway universe, the tyrannosaur and the brontosaur have squared off in a life-and-death confrontation. As they face each other, a floating window suddenly appears between them. When the tyrannosaur peers into the floating mirror, he is startled to see the head of a puny, skinny-looking mammal, with frizzy hair and a tiny face: a human. The head is clearly visible, but it has no body. However, when the brontosaur stares into the same window from the other direction, he sees Fifth Avenue, with its shops and traffic. Then the tyrannosaur finds that this human creature in the window has disappeared, only to appear on the side of the window facing the brontosaur.
Now let us say that suddenly the wind blows our hat into the window. We see the hat sailing into the sky of the other universe, but it is nowhere to be seen along Fifth Avenue. We take one long gulp, and then, in
desperation, we stick our hand into the window to retrieve the hat. As seen by the tyrannosaur, a hat blows out the window, appearing from nowhere. Then he sees a disembodied hand reaching out the window, desperately groping for the hat.
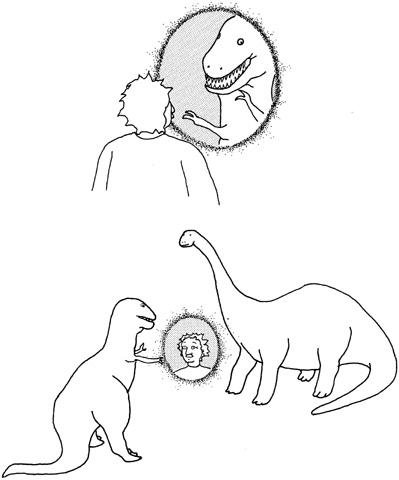
Figure 10.3. In this purely hypothetical example, a “window” or wormhole has opened up in our universe. If we look into the window from one direction, we see one dinosaur. If we look into the other side of the window, we see another dinosaur. As seen from the other universe, a window has opened up between the two dinosaurs. Inside the window, the dinosaurs see a strange small animal (us)
.
