Hyperspace (20 page)
Authors: Michio Kaku,Robert O'Keefe

If quantum theory violates our common sense, it is only because nature does not seem to care much about our common sense. As alien and disturbing as these ideas may seem, they can be readily verified in the laboratory. This is illustrated by the celebrated double-slit experiment. Let us say we fire a beam of electrons at a screen with two small slits. Behind the screen, there is sensitive photographic paper. According to nineteenth-century classical physics, there should be two tiny spots burned into the photographic paper by the beam of electrons behind each hole. However, when the experiment is actually performed in the laboratory, we find an interference pattern (a series of bright and dark lines) on the photographic paper, which is commonly associated with wavelike, not particlelike, behavior (
Figure 5.1
). (The simplest way of creating an interference pattern is to take a quiet bath and then rhythmically splash waves on the water’s surface. The spiderweblike pattern of waves criss-crossing the surface of the water is an interference pattern caused by the collision of many wave fronts.) The pattern on the photographic sheet corresponds to a wave that has penetrated both holes simultaneously and then interfered with itself behind the screen. Since the interference pattern is created by the collective motion of many individual electrons, and since the wave has gone through both holes simultaneously, naively we come to the absurd conclusion that electrons can somehow enter
both holes
simultaneously. But how can an electron be in two places at the same time? According to quantum theory, the electron is indeed a point particle that went through one or the other hole, but the wave function of the electron spread out over space, went through both holes, and then interacted with itself. As unsettling as this idea is, it has been verified repeatedly by experiment. As physicist Sir James Jeans once said, “It is probably as meaningless to discuss how much room an electron takes up as it is to discuss how much room a fear, an anxiety, or an uncertainty takes up.”
1
(A bumper sticker I once saw in Germany summed this up succinctly. It read, “Heisenberg may have slept here.”)
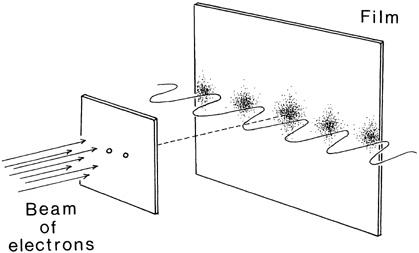
Figure 5.1. A beam of electrons is shot through two small holes and exposes some film. We expect to see two dots on the film. Instead, we find an undulating interference pattern. How can this be? According to quantum theory, the electron is indeed a pointlike particle and cannot go through both holes, but the Schrödinger wave associated with each electron can pass through both holes and interfere with itself
4. There is a finite probability that particles may “tunnel” through or make a quantum leap through impenetrable barriers.
This is one of more stunning predictions of quantum theory. On the atomic level, this prediction has had nothing less than spectacular success. “Tunneling,” or quantum leaps through barriers, has survived every experimental challenge. In fact, a world without tunneling is now unimaginable.
One simple experiment that demonstrates the correctness of quantum tunneling starts by placing an electron in a box. Normally, the electron does not have enough energy to penetrate the walls of the box. If
classical physics is correct, then the electron would never leave the box. However, according to quantum theory, the electron’s probability wave will spread through the box and seep into the outside world. The seepage through the wall can be calculated precisely with the Schrödinger wave equation; that is, there is a small probability that the electron’s position is somewhere
outside
the box. Another way of saying this is that there is a finite but small probability that the electron will tunnel its way through the barrier (the wall of the box) and emerge from the box. In the laboratory, when one measures the rate at which electrons tunnel through these barriers, the numbers agree precisely with the quantum theory.
This quantum tunneling is the secret behind the tunnel diode, which is a purely quantum-mechanical device. Normally, electricity might not have enough energy to penetrate past the tunnel diode. However, the wave function of these electrons can penetrate through barriers in the diode, so there is a non-negligible probability that electricity will emerge on the other side of the barrier by tunneling through it. When you listen to the beautiful sounds of stereo music, remember that you are listening to the rhythms of trillions of electrons obeying this and other bizarre laws of quantum mechanics.
But if quantum mechanics were incorrect, then all of electronics, including television sets, computers, radios, stereo, and so on, would cease to function. (In fact, if quantum theory were incorrect, the atoms in our bodies would collapse, and we would instantly disintegrate. According to Maxwell’s equations, the electrons spinning in an atom should lose their energy within a microsecond and plunge into the nucleus. This sudden collapse is prevented by quantum theory. Thus the fact that we exist is living proof of the correctness of quantum mechanics.)
This also means that there is a finite, calculable probability that “impossible” events will occur. For example, I can calculate the probability that I will unexpectedly disappear and tunnel through the earth and reappear in Hawaii. (The time we would have to wait for such an event to occur, it should be pointed out, is longer than the lifetime of the universe. So we cannot use quantum mechanics to tunnel to vacation spots around the world.)
Quantum physics, after an initial flush of success in the 1930s and 1940s unprecedented in the history of science, began to run out of steam by
the 1960s. Powerful atom smashers built to break up the nucleus of the atom found hundreds of mysterious particles among the debris. Physicists, in fact, were deluged by mountains of experimental data spewing from these particle accelerators.
While Einstein guessed the entire framework of general relativity with only physical intuition, particle physicists were drowning in a mass of experimental data in the 1960s. As Enrico Fermi, one of the builders of the atomic bomb, confessed, “If I could remember the names of all these particles, I would have become a botanist.”
2
As hundreds of “elementary” particles were discovered in the debris of smashed atoms, particle physicists would propose innumerable schemes to explain them, all without luck. So great were the number of incorrect schemes that it was sometimes said that the half-life of a theory of subatomic physics is only 2 years.
Looking back at all the blind alleys and false starts in particle physics during that period, one is reminded of the story of the scientist and the flea.
A scientist once trained a flea to jump whenever he rang a bell. Using a microscope, he then anesthetized one of the flea’s legs and rang the bell again. The flea still jumped.
The scientist then anesthetized another leg and then rang the bell. The flea still jumped.
Eventually, the scientist anesthetized more and more legs, each time ringing the bell, and each time recording that the flea jumped.
Finally, the flea had only one leg left. When the scientist anesthetized the last leg and rang the bell, he found to his surprise that the flea no longer jumped.
Then the scientist solemnly declared his conclusion, based on irrefutable scientific data: Fleas hear through their legs!
Although high-energy physicists have often felt like the scientist in that story, over the decades a consistent quantum theory of matter has slowly emerged. In 1971, the key development that propelled a unified description of three of the quantum forces (excluding gravity) and changed the landscape of theoretical physics was made by a Dutch graduate student, Gerard’t Hooft, who was still in his twenties.
Based on the analogy with photons, the quanta of light, physicists believed that the weak and strong forces were caused by the exchange of a quantum of energy, called the Yang-Mills field. Discovered by C. N. Yang and his student R. L. Mills in 1954, the Yang-Mills field is a generalization of the Maxwell field introduced a century earlier to describe light, except that the Yang-Mills field has many more components and
can have an electrical charge (the photon carries no electrical charge). For the weak interactions, the quantum corresponding to the Yang-Mills field is the
W
particle, which can have charge +1, 0, and −1. For the strong interactions, the quantum corresponding to the Yang-Mills field, the “glue” that holds the protons and neutrons together, was christened the gluon.
Although this general picture was compelling, the problem that bedeviled physicists in the 1950s and 1960s was that the Yang-Mills field is not “renormalizable”; that is, it does not yield finite, meaningful quantities when applied to simple interactions. This rendered quantum theory useless in describing the weak and strong interactions. Quantum physics had hit a brick wall.
This problem arose because physicists, when they calculate what happens when two particles bump into each other, use something called
perturbation theory
, which is a fancy way of saying they use clever approximations. For example, in
Figure 5.2(a)
, we see what happens when an electron bumps into another weakly interacting particle, the elusive neutrino. As a first guess, this interaction can be described by a diagram (called a
Feynman diagram
) showing that a quantum of the weak interactions, the Wparticle, is exchanged between the electron and the neutrino. To a first approximation, this gives us a crude but reasonable fit to the experimental data.
But according to quantum theory, we must also add small quantum corrections to our first guess. To make our calculation rigorous, we must also add in the Feynman diagrams for
all
possible graphs, including ones that have “loops” in them, as in
Figure 5.2(b)
. Ideally, these quantum corrections should be tiny. After all, as we mentioned earlier, quantum theory was meant to give tiny quantum corrections to Newtonian physics. But much to the horror of physicists, these quantum corrections, or “loop graphs,” instead of being small, were infinite. No matter how physicists tinkered with their equations or tried to disguise these infinite quantities, these divergences were persistently found in any calculation of quantum corrections.
Furthermore, the Yang-Mills field had a formidable reputation of being devilishly hard to calculate with, compared with the simpler Maxwell field. There was a mythology surrounding the Yang-Mills field that held that it was simply too complicated for practical calculations. Perhaps it was fortunate that’t Hooft was only a graduate student and wasn’t influenced by the prejudices of more “seasoned” physicists. Using techniques pioneered by his thesis adviser, Martinus Veltman,’t Hooft showed that whenever we have “symmetry breaking” (which we will explain later), the Yang-Mills field acquires a mass but remains a finite theory. He demonstrated that the infinities due to the loop graphs can all be canceled or shuffled around until they become harmless.
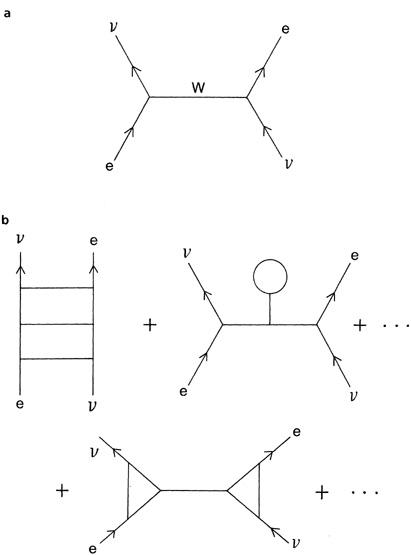
Figure 5.2. (a) In quantum theory, when subatomic particles bump into one another, they exchange packets of energy, or quanta. Electrons and neutrinos interact by exchanging a quantum of the weak force, called the W
particle
. (b) To calculate the complete interaction of electrons and neutrinos, we must add up an infinite series of graphs, called Feynman diagrams, where the quanta are exchanged in increasingly complicated geometric patterns. This process of adding up an infinite series of Feynman graphs is called perturbation theory
.
Almost 20 years after its being proposed by Yang and Mills,’t Hooft finally showed that the Yang-Mills field is a well-defined theory of particle interactions. News of ’t Hooft’s work spread like a flash fire. Nobel laureate Sheldon Glashow remembers that when he heard the news, he exclaimed, “Either this guy’s a total idiot, or he’s the biggest genius to hit physics in years!”
3
Developments came thick and fast. An earlier theory of the weak interactions, proposed in 1967 by Steven Weinberg and Abdus Salam, was rapidly shown to be the correct theory of the weak interactions. By the mid-1970s, the Yang-Mills field was applied to the strong interactions. In the 1970s came the stunning realization that the secret of all nuclear matter could be unlocked by the Yang-Mills field.
