Gödel, Escher, Bach: An Eternal Golden Braid (73 page)
Read Gödel, Escher, Bach: An Eternal Golden Braid Online
Authors: Douglas R. Hofstadter
Tags: #Computers, #Art, #Classical, #Symmetry, #Bach; Johann Sebastian, #Individual Artists, #Science, #Science & Technology, #Philosophy, #General, #Metamathematics, #Intelligence (AI) & Semantics, #G'odel; Kurt, #Music, #Logic, #Biography & Autobiography, #Mathematics, #Genres & Styles, #Artificial Intelligence, #Escher; M. C

times-but not 301.
Now the exact values of all the upper bounds in a program need not be put in numerically by the programmer-indeed, they may not be known in advance. Instead, any upper bound may be determined by calculations carried out
before
its loop is entered. For instance, if you wanted to calculate the value of 2"', there would be two loops. First, you evaluate 3", which involves
n
multiplications. Then, you put 2 to that power, which involves 3"
multiplications. Thus, the upper bound for the second loop is the result of the calculation of the first loop.
Here is how you would express this in a BlooP program:
DEFINE PROCEDURE "TWO-TO-THE-THREE-TO-THE" [N]:
BLOCK 0: BEGIN
CELL(O) <= 1;
LOOP N TIMES:
BLOCK 1: BEGIN
CELL(0) ' 3 x CELL(O);
BLOCK 1: END;
CELL(1) <= 1;
LOOP CELL(O) TIMES:
BLOCK 2: BEGIN
CELL(1) # 2 X CELL(l );
BLOCK 2: END;
OUTPUT <= CELL( I );
BLOCK 0: END.
Conventions of BlooP
Now it is an acquired skill to be able to look at an algorithm written in a computer language, and figure out what it is doing. However, I hope that this algorithm is simple enough that it makes sense without too much
scrutiny. A
procedure
is defined, having one input parameter, N; its output is the desired value.
This procedure definition has what is called
block structure
, which means that certain portions of it are to be considered as units, or blocks. All the statements in a block get executed as a unit. Each block has a number (the outermost being
BLOCK 0)
, and is delimited by a
BEGIN
and an
END
. In our example,
BLOCK 1
and
BLOCK 2
contain just one statement each but shortly you will see longer blocks. A LOOP statement always means to execute the block immediately under it repeatedly. As can be seen above, blocks can be nested.
The strategy of the above algorithm is as described earlier. You begin by taking an auxiliary variable, called
CELL(O)
; you set it initially to 1, and then, in a loop, you multiply it repeatedly by 3 until you've done so exactly
N
times. Next, you do the analogous thing for
CELL(1)
-set it to 1, multiply by 2 exactly
CELL(O)
times, then quit. Finally, you set
OUTPUT
to the value of
CELL(1)
. This is the value returned to the outside world-the only externally visible behavior of the procedure.
A number of points about the notation should be made here. First, the meaning of the left-arrow <= is this:
Evaluate the expression to its right, then take the result and set the
CELL
(or
OUTPUT
) on its left to that value.
So the meaning of a command such as
CELL(1)
<= 3 X
CELL(1)
is to triple the value stored in
CELL(1).
You may think of each
CELL
as being a separate word in the memory of some computer. The only difference between a
CELL
and a true word is that the latter can only hold integers up to some finite limit, whereas we allow a
CELL
to hold any natural number, no matter how big.
Every procedure in BlooP, when called, yields a value-namely the value of the variable called
OUTPUT
. At the beginning of execution of any procedure, it is assumed as a default option that
OUTPUT
has the value 0. That way, even if the procedure never resets
OUTPUT
at all,
OUTPUT
has a well-defined value at all times.
IF-Statements and Branching
Now let us look at another procedure which will show us some other features of BlooP
which give it more generality. How do you find out, knowing only how to add, what the value of
M - N
is? The trick is to add various numbers onto
N
until you find the one which yields
M
. However, what happens if
M
is smaller than
N
? What if we are trying to take
5
from
2
? In the domain of natural numbers, there is no answer. But we would like our B1ooP procedure to give an answer anyway-let's say 0. Here, then, is a BlooP
procedure which does subtraction:
DEFINE PROCEDURE "MINUS" [M,N]:
BLOCK 0: BEGIN
IF M < N, THEN:
QUIT BLOCK 0;
LOOP AT MOST M + 1 TIMES:
BLOCK 1: BEGIN
IF OUTPUT + N = M, THEN:
ABORT LOOP 1;
OUTPUT, <= OUTPUT + 1;
BLOCK 1: END;
BLOCK 0: END.
Here we are making use of the implicit feature that
OUTPUT
begins at 0. If
M
is less than
N
, then the subtraction is impossible, and we simply jump to the bottom of
BLOCK
0
right away, and the answer is 0. That is what is meant by the line
QUIT
BLOCK
0.
But if
M
is not less than
N
, then we skip over that
QUIT
-statement, and carry out the next command in sequence (here, a
LOOP
-statement). That is how IF-statements always work in BlooP.
So we enter
LOOP
1, so called because the block which it tells us to repeat is
BLOCK
1. We try adding 0 to
N
, then 1, 2, etc., until we find a number that gives
M
. At that point, we
ABORT
the loop we are in, meaning we jump to the statement immediately following the
END
which marks the bottom of the loop's block. In this case, that jump brings us just below
BLOCK 1
:
END
, which is to say, to the last statement of the algorithm, and we are done.
OUTPUT
now contains the correct answer.
Notice that there are two distinct instructions for jumping downwards:
QUIT
, and
ABORT
. The former pertains to blocks, the latter to loops.
QUIT BLOCK
n means to jump to the last line of
BLOCK n
, whereas
ABORT LOOP n
means to jump just
below
the last line of
BLOCK n
. This distinction only matters when you are inside a loop and want to continue looping but to quit the block this time around. Then you can say
QUIT
and the proper thing will happen.
Also notice that the words
AT MOST
now precede the upper bound of the loop, which is a warning that the loop may be aborted before the upper bound is reached.
Automatic Chunking
Now there are two last features of BlooP to explain, both of them very important. The first is that, once a procedure has been
defined
, it may be
called
inside later procedure definitions. The effect of this is that
once an operation has been defined in a procedure, it
is considered as simple as a primordial step
. Thus, BlooP features automatic chunking.
You might compare it to the way a good ice skater acquires new motions: not by defining them as long sequences of primordial muscle-actions, but in terms of previously learned motions, which were themselves learned as compounds of earlier
learned motions, etc.-and the nestedness, or chunkedness, can go back many layers until you hit primordial muscle-actions And thus, the repertoire of BlooP programs, like the repertoire of a skater's tricks, grows, quite literally, by loops and bounds.
BlooP Tests
The other feature of BlooP is that certain procedures can have
YES
or
NO
as their output, instead of an integer value. Such procedures are
tests
, rather than
functions
. To indicate the difference, the name of a test must terminate in a question mark. Also, in a test, the default option for
OUTPUT
is not
0
, of course, but
NO
.
Let us see an example of these last two features of BlooP in an algorithm which tests its argument for primality:
DEFINE PROCEDURE "PRIME?" [N]:
BLOCK 0: BEGIN
IF N = 0, THEN:
QUIT BLOCK 0;
CELL(0) <= 2;
LOOP AT MOST MINUS [N,2] TIMES:
BLOCK 1: BEGIN
IF REMAINDER [N,CELL(O)] = 0, THEN:
QUIT BLOCK 0;
CELL(O) <= CELL(O) + 1;
BLOCK 1: END;
OUTPUT <= YES;
BLOCK 0: END.
Notice that I have called two procedures inside this algorithm:
MINUS
and
REMAINDER
. (The latter is presumed to have been previously defined, and you may work out its definition yourself.) Now this test for primality works by trying out potential factors of
N
one by one, starting at
2
and increasing to a maximum of
N - 1
. In case any of them divides
N
exactly (i.e., gives remainder 0), then we jump down to the bottom, and since
OUTPUT
still has its default value at this stage, the answer is
NO
. Only if
N
has no exact divisors will it survive the entirety of
LOOP 1;
then we will emerge smoothly at the statement
OUTPUT <= YES,
which will get executed, and then the procedure is over.
BlooP Programs Contain Chains of Procedures
We have seen how to define procedures in BlooP; however, a procedure definition is only a part of a program. A
program
consists of a
chain of procedure definitions
(each only calling previously defined procedures), optionally followed by one or more
calls
on the procedures defined. Thus, an
example of a full B1ooP program would be the definition of the procedure
TWO-TO-THE-THREE-TO-THE
, followed by the
call
TWO-TO-THE-THREE-TO-THE [2]
which would yield an answer of 512.
If you have only a chain of procedure definitions, then nothing ever gets executed; they are all just waiting for some call, with specific numerical values, to set them in motion. It is like a meat grinder waiting for some meat to grind-or rather, a chain of meat grinders all linked together, each of which is fed from earlier ones ... In the case of meat grinders, the image is perhaps not so savory; however, in the case of BlooP programs, such a construct is quite important, and we will call it a "call-less program". This notion is illustrated in Figure 72.
Now B1ooP is our language for defining predictably terminating calculations. The standard name for
functions
which are B1ooP-computable is
primitive recursive
functions;
and the standard name for
properties
which can be detected by B1ooP-tests is
primitive recursive predicates
. Thus, the function 23n is a primitive recursive function; and the statement "
n
is a prime number" is a primitive recursive predicate.
It is clear intuitively that the Goldbach property is primitive recursive, and to make that quite explicit, here is a procedure definition in BlooP, showing how to test for its presence or absence:
DEFINE PROCEDURE "GOLDBACH?" [N]:
BLOCK 0: BEGIN
CELL(0)
2;
LOOP AT MOST N TIMES:
BLOCK 1: BEGIN
IF {PRIME? [CELL(O)]
AND PRIME? [MINUS [N,CELL(0)]]},
THEN:
BLOCK 2: BEGIN
OUTPUT,# YES;
QUIT BLOCK 0-,
BLOCK 2: END
CELL(0) <= CELL(0) +
BLOCK 1: END;
BLOCK 0: END.
As usual, we assume
NO
until proven
YES
, and we do a brute force search among pairs of numbers which sum up to
N
. If both are prime, we quit the outermost block; otherwise we just go back and try again, until all possibilities are exhausted.
(Warning: The fact that the Goldbach property is primitive recursive does not make the question “Do all numbers have the Goldbach property?” a simple question—far from it!)
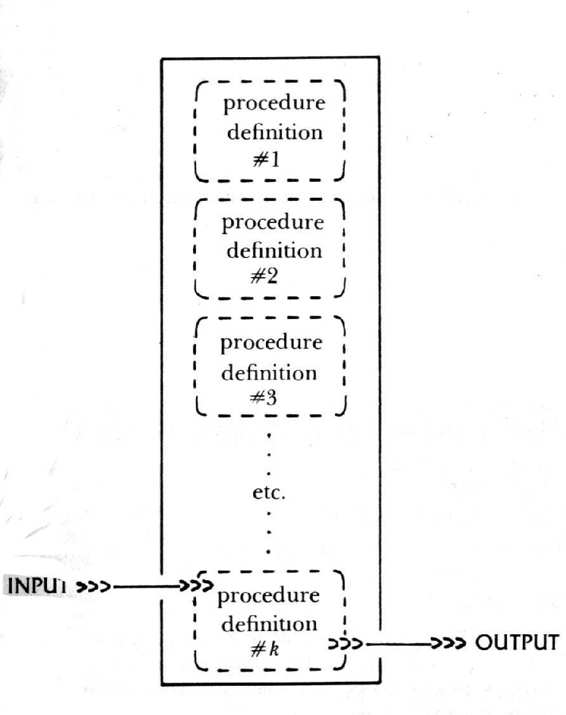
FIGURE 72. The structure of a call-less BlooP program. For this program to be self-contained, each procedure definition may only call procedures defined above it.
Suggested Exercises
Can you write a similar B1ooP procedure which tests for the presence or absence of the Tortoise property (or the Achilles property)? If so, do it. If not, is it merely because you are ignorant about upper bounds, or could it be that there is a fundamental obstacle preventing the formulation of such an algorithm in BlooP? And what about the same questions, with respect to the property of wondrousness, defined in the Dialogue?
