Gödel, Escher, Bach: An Eternal Golden Braid (39 page)

was hotly disputed. It was "proven" to equal 0, 1, ½, and perhaps other values. Out of such controversial findings came a fuller, deeper about infinite series.

A more relevant example is the contradiction right now confronting us-namely the discrepancy between the way we really think, and t the Propositional Calculus imitates us. This has been a source of discomfort for many logicians, and much creative effort has gone into trying to patch up the Propositional Calculus so that it would not act so stupidly and inflexibly. One attempt, put forth in the book
Entailment
by A. R. Anderson and N.

Belnap,3 involves "relevant implication", which tries to make the symbol for "if-then"

reflect genuine causality, or at least connect meanings. Consider the following theorems of the Propositional Calculus

⊃
⊃
P>>

⊃
∨
~P>>

<∧
~P>
⊃
Q>

<⊃
Q>
∨
⊃
P>>

They, and many others like them, all show that there need be no relationship at all between the first and second clauses of an if-then statement for it to be provable within the Propositional Calculus. In protest, "relevant implication" puts certain restrictions on the contexts in which the rules of inference can be applied. Intuitively, it says that

"something can only be derived from something else if they have to do with each other”.

For example, line 10 in the derivation given above would not be allowed in such a system, and that would block the derivation of the
<∧
~P >
⊃
Q>
More radical attempts abandon completely the quest for completeness or consistency, and try to mimic human reasoning with all its inconsistencies. Such research no longer has as its goal to provide a solid underpinning for mathematics, but purely to study human thought processes.

Despite its quirks, the Propositional Calculus has some feat recommend itself. If one embeds it into a larger system (as we will do next Chapter), and if one is sure that the larger system contains no contradictions (and we will be), then the Propositional Calculus does all that one could hope: it provides valid propositional inferences -- all that can be made. So if ever an incompleteness or an inconsistency is uncovered, can be sure that it will be the fault of the larger system, and not of its subsystem which is the Propositional Calculus.

FIGURE 42
. “Crab Canon”, by M. C. Escher (~1965)

Crab Canon

Achilles and the Tortoise happen upon each other

in the park one day while strolling.

Tortoise: Good day, Mr. A.

Achilles: Why, same to you. Tortoise: So nice to run into you. Achilles: That echoes my thoughts.

Tortoise: And it's a perfect day for a walk. I think I'll be walking home soon.

Achilles: Oh, really? I guess there's nothing better for you than w Tortoise: Incidentally, you're looking in very fine fettle these days, I must say.

Achilles: Thank you very much.

Tortoise: Not at all. Here, care for one of my cigars?

Achilles: Oh, you are such a philistine. In this area, the Dutch contributions are of markedly inferior taste, don't you think?

Tortoise: I disagree, in this case. But speaking of taste, I finally saw that Crab Canon by your favorite artist, M. C. Escher, in a gallery the other day, and I fully appreciate the beauty and ingenuity with which he made one single theme mesh with itself going both backwards and forwards. But I am afraid I will always feel Bach is superior to Escher.

Achilles: I don't know. But one thing for certain is that I don't worry about arguments of taste.
De gustibus non est disputandum
.

Tortoise: Tell me, what's it like to be your age? Is it true that one has no worries at all?

Achilles: To be precise, one has no frets.

Tortoise: Oh, well, it's all the same to me.

Achilles: Fiddle. It makes a big difference, you know. Tortoise: Say, don't you play the guitar?

Achilles: That's my good friend. He often plays, the fool. But I myself wouldn't touch a guitar with a ten-foot pole!

(Suddenly, the Crab, appearing from out of nowhere, wanders up excitedly,
pointing to a rather prominent black eye.)

Crab: Hallo! Hulloo! What's up? What's new? You see this bump, this lump? Given to me by a grump. Ho! And on such a fine day. You see, I was just idly loafing about the park when up lumbers this giant fellow from Warsaw-a colossal bear of a man-playing a lute. He was three meters tall, if I'm a day. I mosey on up to the chap, reach skyward and manage to tap him on the knee, saying, "Pardon me, sir, but you are Pole-luting our park with your mazurkas." But wow! he had no sense of humor-not a bit, not a wit-and POW!-he lets loose and belts me one, smack in the eye! Were it in my nature, I would crab up a storm, but in the time-honored tradition of my species, I backed off. After all, when we walk forwards, we move backwards. It's in our genes, you know, turning round and round. That reminds me-I've always wondered, "Which came first-the Crab, or the Gene?" That is to say, "Which came last the Gene, or the Crab?" I'm always turning things round and round, you know. It's in our genes, after all. When we walk backwards, we move forwards. Ah me, oh my! I must lope along on my merry way-so off I go on such a fine day. Sing "ho!" for the life of a Crab!

TATA! iOle!

(And he disappears as suddenly as he arrived.)

Tortoise: That's my good friend. He often plays the fool. But I myself wouldn't touch a ten-foot Pole with a guitar!

Achilles: Say, don't you play the guitar? Tortoise: Fiddle. It makes a big difference, Achilles: Oh, well, it's all the same to me.

Tortoise: To be precise, one has no frets.

Achilles: Tell me, what's it like to be your age? Is it true that one has no worries at all?

Tortoise: I don't know. But one thing for certain is that I don't worry about arguments of taste.
Disputandum non est de gustibus.

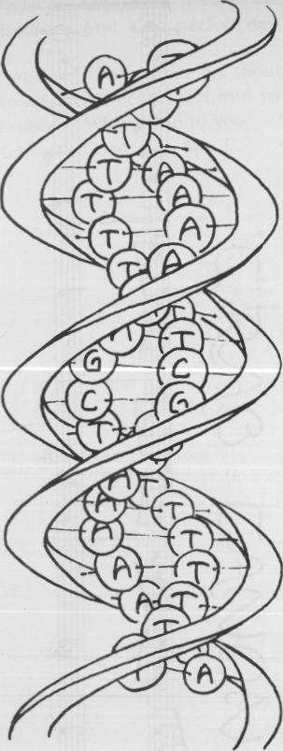
FIGURE 43. Here is a short section one of the Crab's
Genes, turning round and round. When the two DNA

strands are raveled and laid out side by side, they

read this way:

….TTTTTTTTTCGAAAAAAAAA

….AAAAAAAAGCTTTTTTTTTT

Notice that they are the same, only one forwards while

the other goes backwards This is the defining

property of the form called "crab canon" in music. It
is reminiscent of, though a little different from

palindrome, which is a sentence that reads the same

backwards and forwards ,In molecular biology,

such segments of
DNA
are called "palindromes "-a
slight misnomer, since "crab canon" would be more

accurate. Not only is this
DNA
segment crab-

canonical-but moreover its base sequence codes for

the Dialogue's structure Look carefully!

...

Achilles: I disagree, in this case. But speaking of taste, I finally heard that
Crab Canon
by your favorite composer, J. S. Bach, in a concert other day, and I fully appreciate the beauty and ingenuity with which he made one single theme mesh with itself going both backwards and forwards. But I'm afraid I will always feel Escher is superior to Bach

Tortoise: Oh, you are such a philistine. In this area, the Dutch contributions are of markedly inferior taste, don't you think?

Achilles: Not at all. Here, care for one of my cigars?

Tortoise: Thank you very much.

Achilles: Incidentally, you're looking in very fine fettle these days, I must say.

Tortoise: Oh, really? I guess there's nothing better for you than walking.

Achilles: And it's a perfect day for a walk. I think I'll be walking home soon.

Tortoise: That echoes my thoughts.

Achilles: So nice to run into you.

Tortoise: Why, same to you.

Achilles: Good day, Mr. T

Typographical Number Theory

The
Crab Canon
and Indirect Self-Reference

THREE EXAMPLES OF indirect self-reference are found in the Crab Canon. Achilles and the Tortoise both describe artistic creations they know-and, quite accidentally, those creations happen to have the same structure as the Dialogue they're in. (Imagine my surprise, when I, the author, noticed this!) Also, the Crab describes a biological structure and that, too, has the same property. Of course, one could read the Dialogue and understand it and somehow fail to notice that it, too, has the form of a crab canon. This would be understanding it on one level, but not on another. To see the self-reference, one has to look at the form, as well as the content, of the Dialogue.

Gödel’s construction depends on describing the form, as well as the content, of strings of the formal system we shall define in this Chapter --
Typographical Number
Theory (
TNT
). The unexpected twist is that, because of the subtle mapping which Gödel discovered, the form of strings can be described in the formal system itself. Let us acquaint ourselves with this strange system with the capacity for wrapping around.

What We Want to Be Able to Express in TNT

We'll begin by citing some typical sentences belonging to number theory; then we will try to find a set of basic notions in terms of which all our sentences can be rephrased.

Those notions will then be given individual symbols. Incidentally, it should be stated at the outset that the term "number theory" will refer only to properties of positive integers and zero (and sets of such integers). These numbers are called the
natural numbers
.

Negative numbers play no role in this theory. Thus the word "number", when used, will mean exclusively a natural number. And it is important -- vital-for you to keep separate in your mind the formal system (
TNT
) and the rather ill-defined but comfortable old branch of mathematics that is number theory itself; this I shall call "
N
".

Some typical sentences of
N
-number theory-are:

(1)

5 is prime.

(2)

2 is not a square.

(3)

1729 is a sum of two cubes.

(4)

No sum of two positive cubes is itself a cube.

(5)

There are infinitely many prime numbers.

(6)

6 is even.

Now it may seem that we will need a symbol for each notion such as "prime” or "cube"

or "positive" -- but those notions are really not primitive. Primeness, for instance, has to do with the factors which a number has, which in turn has to do with multiplication.

Cubeness as well is defined in terms multiplication. Let us rephrase the sentences, then, in terms of what seem to be more elementary notions.