Gödel, Escher, Bach: An Eternal Golden Braid (117 page)
Read Gödel, Escher, Bach: An Eternal Golden Braid Online
Authors: Douglas R. Hofstadter
Tags: #Computers, #Art, #Classical, #Symmetry, #Bach; Johann Sebastian, #Individual Artists, #Science, #Science & Technology, #Philosophy, #General, #Metamathematics, #Intelligence (AI) & Semantics, #G'odel; Kurt, #Music, #Logic, #Biography & Autobiography, #Mathematics, #Genres & Styles, #Artificial Intelligence, #Escher; M. C

One way to gain some perspective on the nature of this mental metric is to "fight fire with fire". This is done in the Dialogue, where our "subjunctive ability" is asked to imagine a world in which the very notion of
subjunctive ability is slipped, compared to what we expect. In the Dialogue, the first subjunctive instant replay-that where Palindromi stays in bounds-is quite a normal thing to imagine. In fact, it was inspired by a completely ordinary, casual remark made to me by a person sitting next to me at a football game. For some reason it struck me and I wondered what made it seem so natural to slip that particular thing, but not, say, the number of the down, or the present score. From those thoughts, I went on to consider other, probably less slippable features, such as the weather (that's in the Dialogue), the kind of game (also in the Dialogue), and then even loonier variations (also in the Dialogue). I noticed, though, that what was completely ludicrous to slip in one situation could be quite slippable in another. For instance, sometimes you might spontaneously wonder how things would be if the ball had a different shape (e.g., if you are playing basketball with a half-inflated ball); other times that would never enter your mind (e.g., when watching a football game on TV).
Layers of Stability
It seemed to me then, and still does now, that the slippability of a feature of some event (or circumstance) depends on a set of nested contexts in which the event (or circumstance) is perceived to occur. The terms constant, parameter, and variable, borrowed from mathematics, seem useful here. Often mathematicians, physicists, and others will carry out a calculation, saying "c is a constant, p is a parameter, and v is a variable". What they
mean.is that any of them can vary (including the "constant"); however, there is a kind of hierarchy of variability. In the situation which is being represented b~ the symbols, c establishes a global condition; p establishes some less global condition which can vary while c is held fixed; and finally, v can run around while c and p are held fixed. It makes little sense to think of holding v fixed while c and p vary, for c and p establish the context in which v has meaning. For instance, think of a dentist who has a list of patients, and for each patient, a list of teeth. It makes perfect sense (and plenty of money) to hold the patient fixed and vary his teeth-but it makes no sense at all to hold one tooth fixed and vary the patient. (Although sometimes it makes good sense to vary the dentist ...) We build up our mental representation of a situation layer by layer. The lowest layer establishes the deepest aspect of the context-sometimes being so low that it cannot vary at all. For instance, the three-dimensionality of our world is so ingrained that most of us never would imagine letting it slip mentally. It is a constant constant. Then there are layers which establish temporarily, though not permanently, fixed aspects of situations, which could be called background assumptions-things which, in the back of your mind, you know can vary, but which most of the time you unquestioningly accept as unchanging aspects. These could still be called "constants". For instance, when you go to a football game, the rules of the game are constants of that sort. Then there are
"parameters": you think of them as more variable, but you temporarily hold them constant. At a football game, parameters might include the weather, the opposing team, and so forth. There could be-and probably are-several layers of parameters. Finally, we reach the "shakiest" aspects of your mental representation of the situation-the variables.
These are things such as Palindromi's stepping out of bounds, which are mentally "loose"
and which you don't mind letting slip away from their real values, for a short moment.
Frames and Nested Contexts
The word frame is in vogue in Al currently, and it could be defined as a computational instantiation of a context. The term is due to Marvin Minsky, as are many ideas about frames, though the general concept has been floating around for a good number of years.
In frame language, one could say that mental representations of situations involve frames nested within each other. Each of the various ingredients of a situation has its own frame.
It is interesting to verbalize explicitly one of my mental images concerning nested frames. Imagine a large collection of chests of drawers. When you choose a chest, you have a frame, and the drawer holes are places where "subframes" can be attached. But subframes are themselves chests of drawers. How can you stick a whole chest of drawers into the slot for a single drawer in another chest of drawers? Easy: you shrink and distort the second chest, since, after all, this is all mental, not physical. Now in the outer frame, there may be several different drawer slots that need to be
filled; then you may need to fill slots in some of the inner chests of drawers (or subframes). This can go on, recursively.
The vivid surrealistic image of squishing and bending a chest of drawers so that it can fit into a slot of arbitrary shape is probably quite important, because it hints that your concepts are squished and bent by the contexts you force them into. Thus, what does your concept of "person" ', become when the people you are thinking about are football players? It certainly is a distorted concept, one which is forced on you by the overall context. You have stuck the "person" frame into a slot in the "football game" frame. The theory of representing knowledge in frames relies on the idea that the world consists of quasi-closed subsystems, each of which can serve as a context for others without being too disrupted, or creating too much disruption, in the process.
One of the main ideas about frames is that each frame comes with its own set of expectations. The corresponding image is that each chest. of drawers comes with a built-in, but loosely bound, drawer in each of its
drawer slots, called a default. If I tell you, "Picture a river bank", you will invoke a visual image which has various features, most of which you could override if I added extra phrases such as "in a drought" or "in Brazil" or "without a merry-go-round". The existence of default values for slots allows the recursive process of filling slots to come to an end. In effect, you say, "I will fill in the slots myself as far as three layers down; beyond that I will take the default options." Together with its default expectations, a frame contains knowledge of its limits of applicability, and heuristics for switching to other frames in case it has been stretched beyond its limits of tolerance.
The nested structure of a frame gives you a way of "zooming in" and looking at small details from as close up as you wish: you just zoom in on the proper subframe, and then on one of its subframes, etc., until you have the desired amount of detail. It is like having a road atlas of the USA which has a map of the whole country in the front, with individual state maps inside, and even maps of cities and some of the larger towns if you want still more detail. One can imagine an atlas with arbitrary amounts of detail, going down to single blocks, houses, rooms, etc. It is like looking through a telescope with lenses of different power; each lens has its own uses. It is important that one can make use of all the different scales; often detail is irrelevant and even distracting.
Because arbitrarily different frames can be stuck inside other frames' slots, there is great potential for conflict or "collision". The nice neat scheme of a single, global set of layers of "constants", "parameters", and "variables" is an oversimplification. In fact, each frame will have its own hierarchy of variability, and this is what makes analyzing how we perceive such a complex event as a football game, with its many subframes, subsubframes, etc., an incredibly messy operation. How do all these many frames interact with each other? If there is a conflict where one frame says, "This item is a constant" but another frame says, "No, it is a variable!", how does it get resolved? These are deep and difficult problems of frame theory to
which I can give no answers. There has as yet been no complete agreement on what a frame really is, or on how to implement frames in Al programs. I make my own stab at discussing some of these questions in the following section, where I talk about some puzzles in visual pattern recognition, which I call "Bongard problems".
Bongard Problems
Bongard problems
(BP's) are problems of the general type given by the Russian scientist M. Bongard in his book
Pattern Recognition
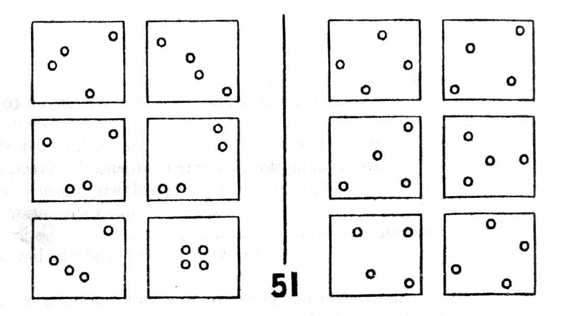
. A typical BP-number 51 in his collection of one hundred-is shown in Figure 119.
FIGURE 119.
Bongard problem 51. From R1. Bongard, Pattern Recognition (Rochelle
Park, N.,J.: Hayden Book Co., Spartan Books, 1970).]
These fascinating problems are intended for pattern-recognizers, whether human or machine. (One might also throw in ETI's-extraterrestrial intelligences.) Each problem consists of twelve boxed figures (henceforth called boxes): six on the left, forming
Class
I
, and six on the right, forming
Class II.
The boxes may be indexed this way: I-A I-B
II-A
II-B
I-C
I-D
II-C
II-D
I-E
I-F
II-E
II-F
The problem is "How do Class I boxes differ from Class II boxes?"
A Bongard problem-solving program would have several stages, in which raw data gradually get converted into descriptions. The early stages are relatively inflexible, and higher stages become gradually more flexible. The final stages have a property which I call
tentativity
, which means simply that the way a picture is represented is always tentative. Upon the drop of a hat, a high-level description can be restructured, using all the devices of the
later stages. The ideas presented below also have a tentative quality to them. I will try to convey overall ideas first, glossing over significant difficulties. Then I will go back and try to explain subtleties and tricks and so forth. So your notion of how it all works may also undergo some revisions as you read. But that is in the spirit of the discussion.
Preprocessing Selects a Mini-vocabulary
Suppose, then, that we have some Bongard problem which we want to solve. The problem is presented to a TV camera and the raw data are read in. Then the raw data are preprocessed. This means that some salient features are detected. The names of these features constitute a "mini-vocabulary" for the problem; they are drawn from a general
"salient-feature vocabulary". Some typical terms of the salient-feature vocabulary are: line segment, curve, horizontal, vertical, black, white, big, small, pointy, round ...
In a second stage of preprocessing, some knowledge about elementary shapes is used; and if any are found, their names are also made available. Thus, terms such as triangle, circle, square, indentation, protrusion, right angle, vertex, cusp, arrow ...
may be selected. This is roughly the point at which the conscious and the unconscious meet, in humans. This discussion is primarily concerned with describing what happens from here on out.
High-Level Descriptions
Now that the picture is "understood", to some extent, in terms of familiar concepts, some looking around is done. Tentative descriptions are made for one or a few of the twelve boxes. They will typically use simple descriptors such as
above, below, to the right of, to the left of, inside, outside of, close to, far from, parallel to, perpendicular to, in a row, scattered, evenly spaced, irregularly spaced, etc.
Also, definite and indefinite numerical descriptors can be used:
1, 2, 3, 4, 5, ... many, few, etc.
More complicated descriptors may be built up, such as
further to the right of, less close to, almost parallel to, etc.

