Games and Mathematics (37 page)
Read Games and Mathematics Online
Authors: David Wells

Transforming structure, transforming perception
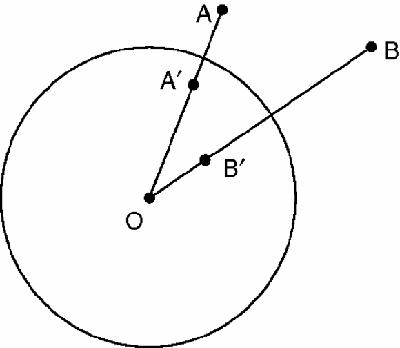

Inversion is an ingenious means of transforming any plane geometrical figure into another using just a reference circle, with centre O, the centre of inversion, and radius
r
(Figure
18.5
).
r
(Figure
18.5
).
Figure 18.5
Inversion in a circle
Inversion in a circle

Given a point, A, its inverse A′ is constructed by joining A to O and then finding A′ on AO such that AO·A′O =
r
2
. (For inversion in 3-D, you use a sphere.)
r
2
. (For inversion in 3-D, you use a sphere.)
Inversion was discovered by Jakob Steiner (1796–1863). It is very powerful because the basic properties of the transformation are so simple:
The power of inversion is illustrated by
Steiner's porism
(Figure
18.6
).
•
A line not through O is inverted into a circle through O, and conversely.
•
A circle not through O is inverted into a circle not through O.
•
A circle in unchanged by inversion if and only if it is orthogonal to the reference circle.
•
The centre of a circle and its inverse circle are in line with O.
•
Angles are unchanged by inversion.
•
Any pair of non-concentric circles can be jointly inverted into a pair of concentric circles.
•
Inversion is its own inverse: the inverse of an inverse, in the same circle, is the original figure.
•
Tangents remain tangents, and tangent circles remain tangent circles.
Steiner's porism
(Figure
18.6
).
Figure 18.6
Starting diagram for Steiner's porism
Starting diagram for Steiner's porism

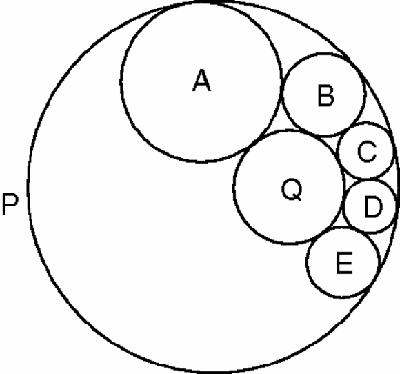
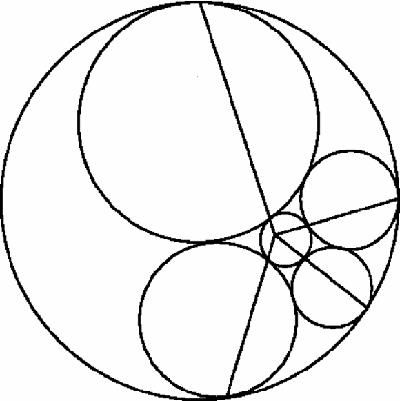
In this figure, P and Q are two non-concentric circles. Circle A has been drawn to touch both, and B drawn to touch A, P and Q. Then C touches B, P and Q, and so on, forming a chain of circles. Steiner's porism says that if and only if the final circle touches A, then it will do so whatever the initial position of A.
Figure
18.7
shows an example. The space between the original two circles P and Q has been filled with a chain of six circles touching in sequence. (This is a perfect subject for animation using Java and a standard geometry package, and many programs will be found on the web in which the entire chain of circles can be slid smoothly between the original circles.)
18.7
shows an example. The space between the original two circles P and Q has been filled with a chain of six circles touching in sequence. (This is a perfect subject for animation using Java and a standard geometry package, and many programs will be found on the web in which the entire chain of circles can be slid smoothly between the original circles.)
Figure 18.7
Steiner's porism
Steiner's porism

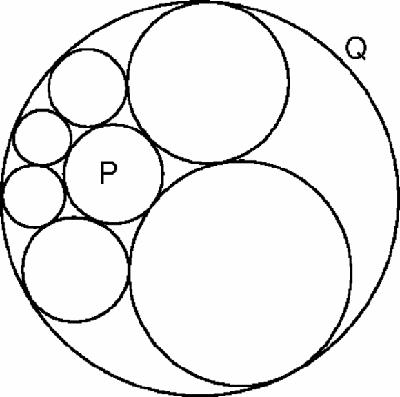
Steiner's
porism
claims that in this chain the last circle will touch the first wherever the first circle is placed. How can this beautiful theorem be proved? Very simply, we choose a point of inversion that will invert the circles P and Q into two
concentric
circles, as in Figure
18.8
. The chain of six
different
circles has becomes a chain of six
identical
circles between P and Q.
porism
claims that in this chain the last circle will touch the first wherever the first circle is placed. How can this beautiful theorem be proved? Very simply, we choose a point of inversion that will invert the circles P and Q into two
concentric
circles, as in Figure
18.8
. The chain of six
different
circles has becomes a chain of six
identical
circles between P and Q.
Fig 18.8
Steiner's porism and proof by inversion
Steiner's porism and proof by inversion

This transformation is always possible – it follows from the basic properties of inversion. Steiner's porism now says that you can rotate the chain of six circles, as if they were identical balls in a mechanical bearing, and indeed this is quite obvious! So Steiner's original porism is true also.
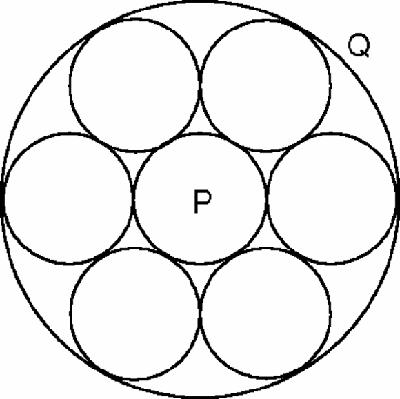
As a footnote, the Steiner's porism diagrams for
N
circles all have extra properties: in Figure
18.9
, eight points of contact have been joined in four pairs: they concur, recalling the Seven Circles Theorem (p. 129).
N
circles all have extra properties: in Figure
18.9
, eight points of contact have been joined in four pairs: they concur, recalling the Seven Circles Theorem (p. 129).
Figure 18.9
Ring of four circles and concurrency
Ring of four circles and concurrency

The four common tangents to consecutive pairs of touching circles in the chain, also concur, at the same point.
Figure 18.10
Ring of four circles and another concurrency
Ring of four circles and another concurrency

These patterns are typical and there are many more which we have not shown. Readers may like to search for them.
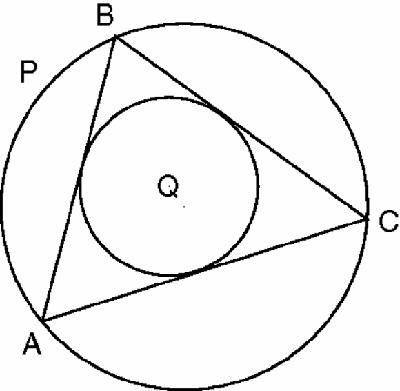
Jean Victor
Poncelet (1788–1867) discovered several very different porisms. In Figure
18.11
, the triangle ABC has its vertices on circle P and its sides touching circle Q. Poncelet's porism says that however vertex A is moved round the circle (e.g. Figure
18.12
), the triangle will still be completed when BC touches the inner circle.
Poncelet (1788–1867) discovered several very different porisms. In Figure
18.11
, the triangle ABC has its vertices on circle P and its sides touching circle Q. Poncelet's porism says that however vertex A is moved round the circle (e.g. Figure
18.12
), the triangle will still be completed when BC touches the inner circle.
Figure 18.11
Poncelet's porism – first position
Poncelet's porism – first position

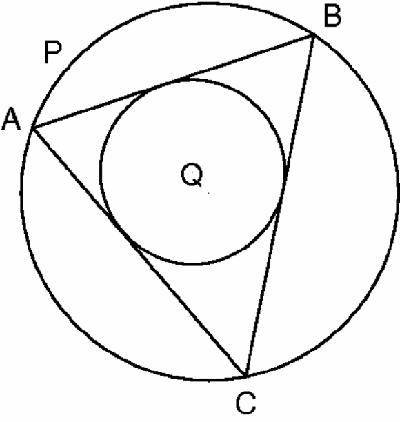
Figure 18.12
Poncelet's porism – second position
Poncelet's porism – second position

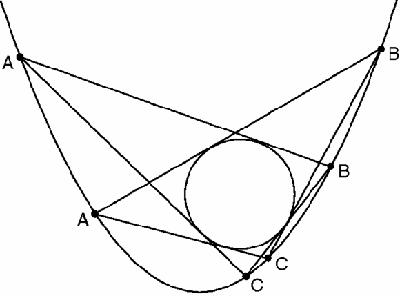
The
‘same’ theorem applies to conics in general: in Figure
18.13
the triangle touches the circle and has its vertices on a parabola
. The vertices A, B and C can be moved at will.
‘same’ theorem applies to conics in general: in Figure
18.13
the triangle touches the circle and has its vertices on a parabola
. The vertices A, B and C can be moved at will.
Figure 18.13
Porism of triangle, circle and parabola [steiner.math.nthu.edu.tw/disk3/cabrijava/poncele t-porism.html]
Porism of triangle, circle and parabola [steiner.math.nthu.edu.tw/disk3/cabrijava/poncele t-porism.html]

Once again, a hidden structure appears and the resulting figure has many of the features that we expect to find in mathematical beauty including simplicity, mystery – or mystery-revealed – and surprise, as well suggesting further questions, such as: where must the circle be placed in relation to the parabola for Poncelet's porism to work?
Other books
Whipped by York, Sabrina
The Man in the Woods by Rosemary Wells
Little Lady Agency and The Prince by Hester Browne
Lives of the Circus Animals by Christopher Bram
Agnes Among the Gargoyles by Patrick Flynn
Chills & Thrills Paranormal Boxed Set by Flynn, Connie
Outsider by Diana Palmer
Werewolves In The Kitchen by Shauna Aura Knight
An Iliad by Alessandro Baricco
Tiona (a sequel to "Vaz") by Laurence Dahners
