From Eternity to Here (55 page)

Figure 67:
Roger Penrose, who has done more than anyone to emphasize the puzzle of the low-entropy early universe.

One of the fields in which Penrose likes to poke holes in cherished beliefs is theoretical cosmology. When I was a graduate student in the late 1980s, theoretical particle physicists and cosmologists mostly took it for granted that some version of inflationary cosmology (discussed in the next chapter) must be true; astronomers tended to be more cautious. Today, this belief is even more common, as evidence from the cosmic microwave background has shown that the small variations in density from place to place in the early universe match very well with what inflation would predict. But Penrose has been consistently skeptical, primarily on the basis of inflation’s failure to explain the low entropy of the early universe. I remember reading one of his papers as a student, and appreciating that Penrose was saying something important but feeling that he had missed the point. It took two decades of thinking about entropy before I became convinced that he has mostly been right all along.

We don’t have a full picture of the space of microstates in quantum gravity, and correspondingly lack a rigorous understanding of entropy. But there is a simple strategy for dealing with this obstacle: We consider what actually happens in the universe. Most of us believe that the evolution of the observable universe has always been compatible with the Second Law, and entropy has been increasing since the Big Bang, even if we’re hazy on the details. If entropy tends to go up, and if there is some process that happens all the time in the universe, but its time-reverse never happens, it probably represents an increase in entropy.

An example of this is “gravitational instability” in the late universe. We’ve been tossing around the notion of “when gravity is important” and “when gravity is not important,” but what is the criterion to decide whether gravity is important? Generally, given some collection of particles, their mutual gravitational forces will always act to pull the particles together—the gravitational force between particles is universally attractive. (In contrast, for example, with electricity and magnetism, which can be either attractive or repulsive depending on what kinds of electric charges you are dealing with.
²³⁸
) But there are other forces, generally collected together under the rubric of “pressure,” that prevent everything from collapsing to a black hole. The Earth or the Sun or an egg doesn’t collapse under its own gravitational pull, because each is supported by the pressure of the material inside it. As a rule of thumb, “gravity is important” means “the gravitational pull of a collection of particles overwhelms the pressure that tries to keep them from collapsing.”

In the very early universe, the temperature is high and the pressure is enormous.
²³⁹
The local gravity between nearby particles is too weak to bring them together, and the initial smoothness of the matter and radiation is preserved. But as the universe expands and cools, the pressure drops, and gravity begins to take over. This is the era of “structure formation,” where the initially smooth distribution of matter gradually begins to condense into stars, galaxies, and larger groups of galaxies. The initial distribution was not perfectly featureless; there were small deviations in density from place to place. In the denser regions, gravity pulled particles even closer together, while the less dense regions lost particles to their denser neighbors and became even emptier. Through gravity’s persistent efforts, what was a highly uniform distribution of matter becomes increasingly lumpy.

Penrose’s point is this: As structure forms in the universe, entropy increases. He puts it this way:

Gravitation is somewhat confusing, in relation to entropy, because of its universally attractive nature. We are used to thinking about entropy in terms of an ordinary gas, where having the gas concentrated in small regions represents
low
entropy . . . and where in the
high
-entropy state of thermal equilibrium, the gas is spread uniformly. But with gravity, things tend to be the other way about. A uniformly spread system of gravitating bodies would represent relatively
low
entropy (unless the velocities of the bodies are enormously high and/or the bodies are very small and/or greatly spread out, so that the gravitational contributions become insignificant), whereas
high
entropy is achieved when the gravitating bodies clump together.
²⁴⁰

All of that is completely correct, and represents an important insight. Under certain conditions, such as those that pertain in the universe on large scales today, even though we don’t have a cut-and-dried formula for the entropy of a system including gravity, we can say with confidence that the entropy increases as structure forms and the universe becomes lumpier.

There is another way of reaching a similar conclusion, through the magic of thought experiments. Take the current macrostate of the universe—some collection of galaxies, dark matter, and so forth, distributed in a certain way through space. But now let’s make a single change: Imagine that the universe is
contracting
rather than expanding. What should happen?

It should be clear that what
won’t
happen is a simple time-reversal of the actual history of the universe from its smooth initial state to its lumpy present—at least, not for the overwhelming majority of microstates within our present macrostate. (If we precisely time-reversed the specific microstate of our present universe, then of course that is exactly what would happen.) If the distribution of matter in our present universe were to start contracting together, individual stars and galaxies would not begin to disperse and smooth out. Instead, the gravitational force between heavy objects would draw them together, and the amount of lumpy structure would actually increase, even as the universe contracted. Black holes would form, and coalesce together to create bigger black holes. There would ultimately be a sort of Big Crunch, but (as Penrose emphasizes) it wouldn’t look anything like the smooth Big Bang from which our universe came. Places where the density was high and black holes formed would crash into a future singularity relatively quickly, while places that were emptier would survive for longer.

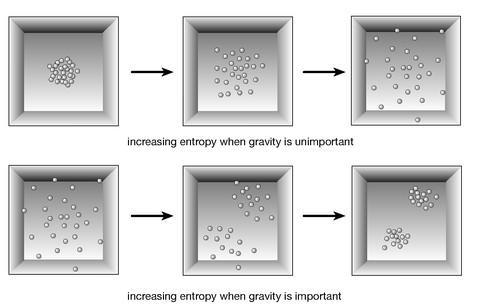
Figure 68:
When gravity is unimportant, increasing entropy tends to smooth things out; when gravity does become important, matter tends to clump together as entropy increases.

This story fits in well with the idea that the space of states within our comoving patch remains fixed, but when the universe is small most of the states cannot be described as vibrating quantum fields in an otherwise smooth space. Such a picture would be completely inadequate to describe the chaotic black-hole-filled mess that we would generically expect from a collapsing universe. But such a messy configuration is just as much an allowed state of the universe as the relatively smooth backgrounds we traditionally deal with in cosmology. Indeed, such a configuration has a higher entropy than a smooth universe (which we know because a collapsing universe would generically evolve into something messy), which means that there are many more microstates of that form than of the form where everything is relatively smooth. Why our actual universe is so atypical is, of course, at the heart of our mystery.

THE EVOLUTION OF ENTROPY

We’ve now assembled enough background knowledge to follow Penrose and take a stab at quantifying how the entropy of our universe changes from early times to today. We know the basic story of how our comoving patch evolves—at early times it was small, and full of hot, dense gas that was very close to perfectly smooth, and at later times it is larger and cooler and more dilute, and contains a distribution of stars and galaxies that is quite lumpy on small scales, although it’s still basically smooth over very large distances. So what is its entropy?

At early times, when things were smooth, we can calculate the entropy by simply ignoring the influence of gravity. This might seem to go against the philosophy I’ve thus far been advocating, but we’re not saying that gravity is irrelevant in principle—we’re simply taking advantage of the fact that, in practice, our early universe was in a configuration where the gravitational forces between particles didn’t play a significant role in the dynamics. Basically, it was just a box of hot gas. And a box of hot gas is something whose entropy we know how to calculate.

The entropy of our comoving patch of space when it was young and smooth is:

S
_early
≈ 10
⁸⁸
.

The “≈” sign means “approximately equal to,” as we want to emphasize that this is a rough estimate, not a rigorous calculation. This number comes from simply treating the contents of the universe as a conventional gas in thermal equilibrium, and plugging in the formulas worked out by thermodynamicists in the nineteenth century, with one additional feature: Most of the particles in the early universe are photons and neutrinos, moving at or close to the speed of light, so relativity is important. Up to some numerical factors that don’t change the answer very much, the entropy of a hot gas of relativistic particles is simply equal to the total number of such particles. There are about 10
⁸⁸
particles within our comoving patch of universe, so that’s what the entropy was at early times. (It increases a bit along the way, but not by much, so treating the entropy as approximately constant at early times is a good approximation.)

Today, gravity has become important. It is not very accurate to think of the matter in the universe as a gas in thermal equilibrium with negligible gravity; ordinary matter and dark matter have condensed into galaxies and other structures, and the entropy has increased considerably. Unfortunately, we don’t have a reliable formula that tracks the change in entropy during the formation of a galaxy.

What we do have is a formula for the circumstance in which gravity is at its most important: in a black hole. As far as we know, very little of the total mass of the universe is contained in the form of black holes.
²⁴¹
In a galaxy like the Milky Way, there are a number of stellar-sized black holes (with maybe 10 times the mass of the Sun each), but the majority of the total black hole mass is in the form of a single supermassive black hole at the galactic center. While supermassive black holes are certainly big—often over a million times the mass of the Sun—that’s nothing compared to an entire galaxy, where the total mass might be 100 billion times the mass of the Sun.

But while only a tiny fraction of the mass of the universe appears to be in black holes, they contain a huge amount of entropy. A single supermassive black hole, a million times the mass of the Sun, has an entropy according to the Bekenstein-Hawking formula of 10
⁹⁰
. That’s a hundred times larger than all of the nongravitational entropy in all the matter and radiation in the observable universe.
²⁴²

Even though we don’t have a good understanding of the space of states of gravitating matter, it’s safe to say that the total entropy of the universe today is mostly in the form of these supermassive black holes. Since there are about 100 billion (10
¹¹
) galaxies in the universe, it’s reasonable to approximate the total entropy by assuming 100 billion such black holes. (They might be missing from some galaxies, but other galaxies will have larger black holes, so this is not a bad approximation.) With an entropy of 10
⁹⁰
per million-solar-mass black hole, that gives us a total entropy within our comoving patch today of

S
_today
≈ 10
¹⁰¹
.

Mathematician Edward Kasner coined the term
googol
to stand for 10
¹⁰⁰
, a number he used to convey the idea of an unimaginably big quantity. The entropy of the universe today is about ten googols. (The folks from Google used this number as an inspiration for the name of their search engine; now it’s impossible to refer to a googol without being misunderstood.)

When we write the current entropy of our comoving patch as 10
¹⁰¹
, it doesn’t seem all that much larger than its value in the early universe, 10
⁸⁸
. But that’s just the miracle of compact notation. In fact, 10
¹⁰¹
is ten trillion (10
¹³
) times bigger than 10
⁸⁸
. The entropy of the universe has increased by an enormous amount since the days when everything was smooth and featureless.