From Eternity to Here (27 page)

In the real world,
apparent
loss of information happens all the time. Consider two different states of a glass of water. In one state, the water is uniform and at the

Figure 40:
Apparent loss of information in a glass of water. A future state of a glass of cool water could have come either from the same state of cool water, or from warm water with an ice cube.
same cool temperature; in the other, we have warm water but also an ice cube. These two states can evolve into the future into what appears to be the same state: a glass of cool water.
We’ve encountered this phenomenon before: It’s the arrow of time. Entropy increases as the ice melts into the warm water; that’s a process that can happen but will never un-happen. The puzzle is that the motion of the individual molecules making up the water is perfectly invariant under time reversal, while the macroscopic description in terms of ice and liquid is not. To understand how reversible underlying laws give rise to macroscopic irreversibility, we must return to Boltzmann and his ideas about entropy.
8
ENTROPY AND DISORDER
Nobody can imagine in physical terms the act of reversing the order of time. Time is not reversible.
—Vladimir Nabokov, Look at the Harlequins!
Why is it that discussions of entropy and the Second Law of Thermodynamics so often end up being about food? Here are some popular (and tasty) examples of the increase of entropy in irreversible processes:
• Breaking eggs and scrambling them.
• Stirring milk into coffee.
• Spilling wine on a new carpet.
• The diffusion of the aroma of a freshly baked pie into a room.
• Ice cubes melting in a glass of water.
To be fair, not all of these are equally appetizing; the ice-cube example is kind of bland, unless you replace the water with gin. Furthermore, I should come clean about the scrambled-eggs story. The truth is that the act of cooking the eggs in your skillet isn’t a straightforward demonstration of the Second Law; the cooking is a chemical reaction that is caused by the introduction of heat, which wouldn’t happen if the eggs weren’t an open system. Entropy comes into play when we break the eggs and whisk the yolks together with the whites; the point of cooking the resulting mixture is to avoid salmonella poisoning, not to illustrate thermodynamics.
The relationship between entropy and food arises largely from the ubiquity of
mixing
. In the kitchen, we are often interested in combining together two things that had been kept separate—either two different forms of the same substance (ice and liquid water) or two altogether different ingredients (milk and coffee, egg whites and yolks). The original nineteenth-century thermodynamicists were extremely interested in the dynamics of heat, and the melting ice cube would have been of foremost concern to them; they would have been less fascinated by processes where all the ingredients were at the same temperature, such as spilling wine onto a carpet. But clearly there is some underlying similarity in what is going on; an initial state in which substances are kept separate evolves into a final state in which they are mixed together. It’s easy to mix things and hard to unmix them—the arrow of time looms over everything we do in the kitchen.
Why is mixing easy and unmixing hard? When we mix two liquids, we see them swirl together and gradually blend into a uniform texture. By itself, that process doesn’t offer much clue into what is really going on. So instead let’s visualize what happens when we mix together two different kinds of colored sand. The important thing about sand is that it’s clearly made of discrete units, the individual grains. When we mix together, for example, blue sand and red sand, the mixture as a whole begins to look purple. But it’s not that the individual grains turn purple; they maintain their identities, while the blue grains and the red grains become jumbled together. It’s only when we look from afar (“macroscopically”) that it makes sense to think of the mixture as being purple; when we peer closely at the sand (“microscopically”) we see individual blue and red grains.
The great insight of the pioneers of kinetic theory—Daniel Bernoulli in Swit zerland, Rudolf Clausius in Germany, James Clerk Maxwell and William Thomson in Great Britain, Ludwig Boltzmann in Austria, and Josiah Willard Gibbs in the United States—was to understand all liquids and gases in the same way we think of sand: as collections of very tiny pieces with persistent identities. Instead of grains, of course, we think of liquids and gases as composed of atoms and molecules. But the principle is the same. When milk and coffee mix, the individual milk molecules don’t combine with the individual coffee molecules to make some new kind of molecule; the two sets of molecules simply intermingle. Even heat is a property of atoms and molecules, rather than constituting some kind of fluid in its own right—the heat contained in an object is a measure of the energy of the rapidly moving molecules within it. When an ice cube melts into a glass of water, the molecules remain the same, but they gradually bump into one another and distribute their energy evenly throughout the molecules in the glass.
Without (yet) being precise about the mathematical definition of “entropy,” the example of blending two kinds of colored sand illustrates why it is easier to mix things than to unmix them. Imagine a bowl of sand, with all of the blue grains on one side of the bowl and the red grains on the other. It’s pretty clear that this arrangement is somewhat
delicate
—if we disturb the bowl by shaking it or stirring with a spoon, the two colors will begin to mix together. If, on the other hand, we start with the two colors completely mixed, such an arrangement is
robust
—if we disturb the mixture, it will stay mixed. The reason is simple: To separate out two kinds of sand that are mixed together requires a much more precise operation than simply shaking or stirring. We would have to reach in carefully with tweezers and a magnifying glass to move all of the red grains to one side of the bowl and all of the blue grains to the other. It takes much more care to create the delicate unmixed state of sand than to create the robust mixed state.
That’s a point of view that can be made fearsomely quantitative and scientific, which is exactly what Boltzmann and others managed to do in the 1870s. We’re going to dig into the guts of what they did, and explore what it explains and what it doesn’t, and how it can be reconciled with underlying laws of physics that are perfectly reversible. But it should already be clear that a crucial role is played by the
large numbers
of atoms that we find in macroscopic objects in the real world. If we had only one grain of red sand and one grain of blue sand, there would be no distinction between “mixed” and “unmixed.” In the last chapter we discussed how the underlying laws of physics work equally well forward or backward in time (suitably defined). That’s a microscopic description, in which we keep careful track of each and every constituent of a system. But very often in the real world, where large numbers of atoms are involved, we don’t keep track of nearly that much information. Instead, we make simplifications—thinking about the average color or temperature or pressure, rather than the specific position and momentum of each atom. When we think macroscopically, we forget (or ignore) detailed information about every particle—and that’s where entropy and irreversibility begin to come into play.
SMOOTHING OUT
The basic idea we want to understand is “how do macroscopic features of a system made of many atoms evolve as a consequence of the motion of the individual atoms?” (I’ll use “atoms” and “molecules” and “particles” more or less interchangeably, since all we care is that they are tiny things that obey reversible laws of physics, and that you need a lot of them to make something macroscopic.) In that spirit, consider a sealed box divided in two by a wall with a hole in it. Gas molecules can bounce around on one side of the box and will usually bounce right off the central wall, but every once in a while they will sneak through to the other side. We might imagine, for example, that the molecules bounce off the central wall 995 times out of 1,000, but one-half of 1 percent of the time (each second, let’s say) they find the hole and move to the other side.

Figure 41:
A box of gas molecules, featuring a central partition with a hole. Every second, each molecule has a tiny chance to go through the hole to the other side.
This example is pleasingly specific; we can examine a particular instance in detail and see what happens.
123
Every second, each molecule on the left side of the box has a 99.5 percent chance of staying on that side, and a 0.5 percent chance of moving to the other side; likewise for the right side of the box. This rule is perfectly time-reversal invariant; if you made a movie of the motion of just one particle obeying this rule, you couldn’t tell whether it was being run forward or backward in time. At the level of individual particles, we can’t distinguish the past from the future.
In Figure 42 we have portrayed one possible evolution of such a box; time moves upward, as always. The box has 2,000 “air molecules” in it, and starts at time
t
= 1 with 1,600 molecules on the left-hand side and only 400 on the right. (You’re not supposed to ask
why
it starts that way—although later, when we replace “the box” with “the universe,” we will start asking such questions.) It’s not very surprising what happens as we sit there and let the molecules bounce around inside the box. Every second, there is a small chance that any particular molecule will switch sides; but, because we started with a much larger number of molecules on the one side, there is a general tendency for the numbers to even out. (Exactly like temperature, in Clausius’s formulation of the Second Law.) When there are more molecules on the left, the total number of molecules that shift from left to right will usually be larger than the number that shift from right to left. So after 50 seconds we see that the numbers are beginning to equal out, and after 200 seconds the distribution is essentially equal.
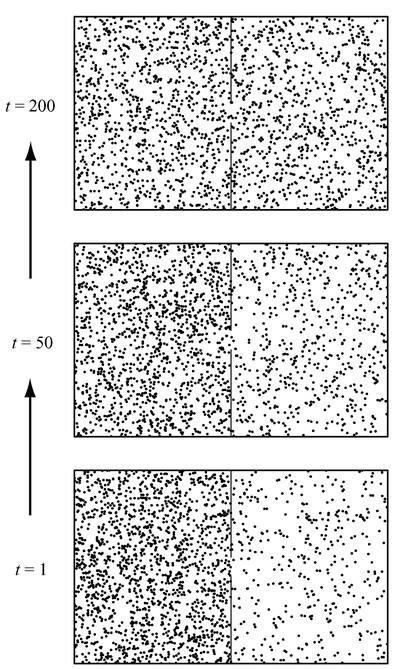
Figure 42:
Evolution of 2,000 molecules in a divided box of gas. We start with 1,600 molecules on the left, 400 on the right. After 50 seconds, there are about 1,400 on the left and 600 on the right; by the time 200 seconds have passed, the molecules are distributed equally between the two sides.
This box clearly displays an arrow of time. Even if we hadn’t labeled the different distributions in the figure with the specific times to which they corresponded, most people wouldn’t have any trouble guessing that the bottom box came first and the top box came last. We’re not surprised when the air molecules even themselves out, but we’d be very surprised if they spontaneously congregated all (or even mostly) on one side of the box. The past is the direction of time in which things were more segregated, while the future is the direction in which they have smoothed themselves out. It’s exactly the same thing that happens when a teaspoon of milk spreads out into a cup of coffee.
