From Eternity to Here (15 page)

Relativity is different. The Newtonian rule “you must move forward in time” is replaced by a new rule: You must move more slowly than the speed of light. (Unless you are a photon or another massless particle, in which case you always move exactly at the speed of light if you are in empty space.) And the structure we were able to impose on Newtonian spacetime, in the form of a unique slicing into moments of constant time, is replaced by another kind of structure:
light cones
.

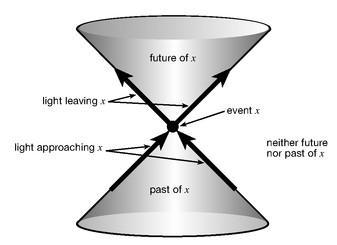
Figure 14:
Spacetime in the vicinity of a certain event
x
. According to relativity, every event comes with a light cone, defined by considering all possible paths light could take to or from that point. Events outside the light cone cannot unambiguously be labeled “past” or “future.”

Light cones are conceptually pretty simple. Take an event, a single point in spacetime, and imagine all of the different paths that light could take to or from that event; these define the light cone associated with that event. Hypothetical light rays emerging from the event define a future light cone, while those converging on the event define a past light cone, and when we mean both we just say “the light cone.” The rule that you can’t move faster than the speed of light is equivalent to saying that your world line must remain inside the light cone of every event through which it passes. World lines that do this, describing slower-than-light objects, are called “timelike”; if somehow you could move faster than light, your world line would be “spacelike,” since it was covering more ground in space than in time. If you move exactly at the speed of light, your world line is imaginatively labeled “lightlike.”

Starting from a single event in Newtonian spacetime, we were able to define a surface of constant time that spread uniquely throughout the universe, splitting the set of all events into the past and the future (plus “simultaneous” events precisely on the surface). In relativity we can’t do that. Instead, the light cone associated with an event divides spacetime into the past of that event (events inside the past light cone), the future of that event (inside the future light cone), the light cone itself, and a bunch of points outside the light cone that are neither in the past nor in the future.

Figure 15:
Light cones replace the moments of constant time from Newtonian spacetime. World lines of massive particles must come to an event from inside the past light cone, and leave inside the future light cone—a timelike path. Spacelike paths move faster than light and are therefore not allowed.

It’s that last bit that really gets people. In our reflexively Newtonian way of thinking about the world, we insist that some faraway event happened either in the past, or in the future, or at the same time as some event on our own world line. In relativity, for spacelike separated events (outside one another’s light cones), the answer is “none of the above.” We could
choose
to draw some surfaces that sliced through spacetime and label them “surfaces of constant time,” if we really wanted to. That would be taking advantage of the definition of time as a coordinate on spacetime, as discussed in Chapter One. But the result reflects our personal choice, not a real feature of the universe. In relativity, the concept of “simultaneous faraway events” does not make sense.
⁶⁷

There is a very strong temptation, when drawing maps of spacetime such as shown in Figure 15, to draw a vertical axis labeled “time,” and a horizontal axis (or two) labeled “space.” The absence of those axes on our version of the spacetime diagram is completely intentional. The whole point of spacetime according to relativity is that it is not fundamentally divided up into “time” and “space.” The light cones, demarcating the accessible past and future of each event, are not added on top of the straightforward Newtonian decomposition of spacetime into time and space; they
replace
that structure entirely. Time can be measured along each individual world line, but it’s not a built-in feature of the entire spacetime.

It would be irresponsible to move on without highlighting one other difference between time and space: There is only one dimension of time, whereas there are three dimensions of space.
⁶⁸
We don’t have a good understanding of why this should be so. That is, our understanding of fundamental physics isn’t sufficiently developed to state with confidence whether there is some reason why there couldn’t be more than one dimension of time, or for that matter zero dimensions of time. What we do know is that life would be very different with more than one time dimension. With only one such dimension, physical objects (which move along timelike paths) can’t help but move along that particular direction. If there were more than one, nothing would force us to move forward in time; we could move in circles, for example. Whether or not one can build a consistent theory of physics under such conditions is an open question, but at the least, things would be different.

EINSTEIN’S MOST FAMOUS EQUATION

Einstein’s major 1905 paper in which he laid out the principles of special relativity, “On the Electrodynamics of Moving Bodies,” took up thirty pages in
Annalen der Physik
, the leading German scientific journal of the time. Soon thereafter, he published a two-page paper entitled “Does the Inertia of a Body Depend upon Its Energy Content?”
⁶⁹
The purpose of this paper was to point out a straightforward but interesting consequence of his longer work: The energy of an object at rest is proportional to its mass. (Mass and inertia are here being used interchangeably.) That’s the idea behind what is surely the most famous equation in history,

E
=
mc
²
.

Let’s think about this equation carefully, as it is often misunderstood. The factor
c
²
is of course the speed of light squared. Physicists learn to think,
Aha, relativity must be involved,
whenever they see the speed of light in an equation. The factor
m
is the mass of the object under consideration. In some places you might read about the “relativistic mass,” which increases when an object is in motion. That’s not really the most useful way of thinking about things; it’s better to consider
m
as the once-and-for-all mass that an object has when it is at rest. Finally,
E
is not exactly “the energy”; in this equation, it specifically plays the role of the energy of an object at rest. If an object is moving, its energy will certainly be higher.

So Einstein’s famous equation tells us that the energy of an object when it is at rest is equal to its mass times the speed of light squared. Note the importance of the innocuous phrase
an object
. Not everything in the world is an object! For example, we’ve already spoken of dark energy, which is responsible for the acceleration of the universe. Dark energy doesn’t seem to be a collection of particles or other objects; it pervades spacetime smoothly. So as far as dark energy is concerned,
E = mc
²
simply doesn’t apply. Likewise, some objects (such as a photon) can never be at rest, since they are always moving at the speed of light. In those cases, again, the equation isn’t applicable.

Everyone knows the practical implication of this equation: Even a small amount of mass is equivalent to a huge amount of energy. (The speed of light, in everyday units, is a really big number.) There are many forms of energy, and what special relativity is telling us is that mass is one form that energy can take. But the various forms can be converted back and forth into one another, which happens all the time. The domain of validity of
E = mc
²
isn’t limited to esoteric realms of nuclear physics or cosmology; it’s applicable to every kind of object at rest, on Mars or in your living room. If we take a piece of paper and burn it, letting the photons produced escape along with their energy, the resulting ashes will have a slightly lower mass (no matter how careful we are to capture all of them) than the combination of the original paper plus the oxygen it used to burn.
E = mc
²
isn’t just about atomic bombs; it’s a profound feature of the dynamics of energy all around us.

5

TIME IS FLEXIBLE

The reason why the universe is eternal is that it does not live for itself; it gives life to others as it transforms.

—Lao Tzu, Tao Te Ching

The original impetus behind special relativity was not a puzzling experimental result (although the Michelson-Morley experiment certainly was that); it was an apparent conflict between two preexisting theoretical frameworks.
⁷⁰
On the one hand you had Newtonian mechanics, the gleaming edifice of physics on which all subsequent theories had been based. On the other hand you had James Clerk Maxwell’s unification of electricity and magnetism, which came about in the middle of the nineteenth century and had explained an impressive variety of experimental phenomena. The problem was that these two marvelously successful theories didn’t fit together. Newtonian mechanics implied that the relative velocity of two objects moving past each other was simply the sum of their two velocities; Maxwellian electromagnetism implied that the speed of light was an exception to this rule. Special relativity managed to bring the two theories together into a single whole, by providing a framework for mechanics in which the speed of light did play a special role, but which reduced to Newton’s model when particles were moving slowly.

Like many dramatic changes of worldview, the triumph of special relativity came at a cost. In this case, the greatest single success of Newtonian physics—his theory of gravity, which accounted for the motions of the planets with exquisite precision—was left out of the happy reconciliation. Along with electromagnetism, gravity is the most obvious force in the universe, and Einstein was determined to fit it in to the language of relativity. You might expect that this would involve modifying a few equations here and there to make Newton’s equations consistent with invariance under boosts, but attempts along those lines fell frustratingly short.

Eventually Einstein hit on a brilliant insight, essentially by employing the spaceship thought experiment we’ve been considering. (He thought of it first.) In describing our travels in this hypothetical sealed spaceship, I was careful to note that we are far away from any gravitational fields, so we wouldn’t have to worry about falling into a star or having our robot probes deflected by the pull of a nearby planet. But what if we were near a prominent gravitational field? Imagine our ship was, for example, in orbit around the Earth. How would that affect the experiments we were doing inside the ship?

Einstein’s answer was: They wouldn’t affect them at all, as long as we confined our attention to relatively small regions of space and brief intervals of time. We can do whatever kinds of experiments we like—measuring the rates of chemical reactions, dropping balls and watching how they fall, observing weights on springs—and we would get exactly the same answer zipping around in low-Earth orbit as we would in the far reaches of interstellar space. Of course if we wait long enough we can tell we are in orbit; if we let a fork and a spoon freely float in front of our noses, with the fork just slightly closer to the Earth, the fork will then feel just a slightly larger gravitational pull, and therefore move just ever so slightly away from the spoon. But effects like that take time to accumulate; if we confine our attention to sufficiently small regions of space and time, there isn’t any experiment we can imagine doing that could reveal the presence of the gravitational pull keeping us in orbit around the Earth.