For the Love of Physics (28 page)
Read For the Love of Physics Online
Authors: Walter Lewin
Tags: #Biography & Autobiography, #Science & Technology, #Science, #General, #Physics, #Astrophysics, #Essays

I think the name
gravitational potential energy
is an excellent name. Think of it this way. If I pick the book up from the floor and place it on the shelf, it takes 19.6 joules of my energy to do so. Is this energy lost?
No!
Now that the book is 2 meters above the floor, it has the “potential” of returning that energy back to me in the form of kinetic energy—whenever I drop it on the floor, be it the next day or the next year! The higher the book is above the floor, the more energy is “potentially” available, but, of course I have to provide that extra energy to place the book higher.
In a similar way, it takes energy to pull the string of a bow back when you want to shoot an arrow. That energy is stored in the bow and it is “potentially” available, at a time of your chosing, to convert that potential energy into kinetic energy, which gives the arrow its speed.
Now, there is a simple equation I can use to show you something
quite wonderful. If you bear with me for just a bit of math, you’ll see why Galileo’s most famous (non)experiment works. Recall that he was said to have dropped balls of different mass (thus different weight) from the Leaning Tower of Pisa to show that their rate of falling was independent of their mass. It follows from Newton’s laws of motion that the kinetic energy (KE) of a moving object is proportional both to the mass of the object and to the square of its speed; the equation for that is
KE
= 1/2
mv
2
. And since we know that the change in gravitational potential energy of the object is converted to kinetic energy, then we can say that
mgh
equals 1/2
mv
2
, so you have the equation
mgh
= 1/2
mv
2
. If you divide both sides by
m, m
disappears from the equation entirely, and you have
gh
= 1/2
v
2
. Then to get rid of the fraction we multiply both sides of the equation by 2, to get 2
gh
=
v
2
. This means that
v
, the speed, which is what Galileo was testing for, equals the square root of 2
gh
.
*
And note that mass has completely disappeared from the equation! It is literally not a factor—the speed does not depend on the mass. To take a specific example, if we drop a rock (of any mass) from a height of 100 meters, in the absence of air drag it will hit the ground with a speed of about 45 meters per second, or about 100 miles per hour.
Imagine a rock (of any mass) falling from a few hundred thousand miles away to the Earth. With what speed would it enter the Earth’s atmosphere? Unfortunately, we cannot use the above simple equation that the speed is the square root of 2
gh
because the gravitational acceleration depends strongly on the distance to Earth. At the distance of the Moon (about 240,000 miles), the gravitational acceleration due to Earth is about 3,600 times smaller than what it is close to the surface of the Earth. Without showing you the math, take my word for it, the speed would be about 25,000 miles per hour!
Perhaps you can now understand how important gravitational potential energy is in astronomy. As I will discuss in
chapter 13
, when matter
falls from a large distance onto a neutron star, it crashes onto the neutron star with a speed of roughly 100,000 miles per second, yes, per second! If the rock had a mass of only 1 kilogram, its kinetic energy would then be about 13 thousand trillion (13 × 10
15
) joules, which is roughly the amount of energy that a large (1,000 MW) power plant produces in about half a year.
The fact that different types of energy can be converted into one another and then back again is remarkable enough, but what is even more spectacular is that there is never any net loss of energy. Never. Amazing. This is why the wrecking ball has never killed me.
When I pull the 15 kilogram ball up to my chin over a vertical distance
h
, I increase its gravitational potential energy by
mgh.
When I drop the ball, it begins to swing across the room due to the force of gravity, and
mgh
is converted into kinetic energy. Here,
h
is the vertical distance between my chin and the lowest position of the bob at the end of the string. As the ball reaches its lowest point in the swing, its kinetic energy will be
mgh.
As the ball completes its arc and reaches the upper limit of its swing, that kinetic energy is converted back into potential energy—which is why, at the very height of a pendulum swing, the ball stops for a moment. If there’s no kinetic energy, there’s no movement. But that is for just the slightest moment, because then the ball goes back down again, on its reverse swing, and potential energy is converted again into kinetic energy. The sum of kinetic energy and potential energy is called mechanical energy, and in the absence of friction (in this case air drag on the bob), the total mechanical energy does not change—it is conserved.
This means that the ball can go no higher than the exact spot from which it was released—as long as no extra energy is imparted to it anywhere along the way. Air drag is my safety cushion. A
very
small amount of the mechanical energy of the pendulum is sucked away by air drag and converted into heat. As a result, the bob stops just one-eighth of an inch from my chin, as you can see in the video of lecture 11 from course 8.01. Susan has seen me do the demonstration three times—she shivers each time. Someone once asked me if I practiced a lot, and I always
answer with what is true: that I do not have to practice as I trust the conservation of energy, 100 percent.
But if I were to give the ball the slightest little push when I let it go—say I had coughed just then and that caused me to give the ball some thrust—it would swing back to a spot a little higher than where I released it from, smashing into my chin.
The conservation of energy was discovered largely due to the work of a mid-nineteenth-century English brewer’s son, James Joule. So important was his work to understanding the nature of energy that the international unit by which energy is measured, the joule, was named after him. His father had sent him and his brother to study with the famous experimental scientist John Dalton. Clearly Dalton taught Joule well. After Joule inherited his father’s brewery, he performed a host of innovative experiments in the brewery’s basement, probing in ingenious ways into the characteristics of electricity, heat, and mechanical energy. One of his discoveries was that electric current produces heat in a conductor, which he found by putting coils of different kinds of metal with current running through them into jars of water and measuring their changes in temperature.
Joule had the fundamental insight that heat is a form of energy, which refuted what had been the widely accepted understanding of heat for many years. Heat, it was thought, was a kind of fluid, which was called caloric—from which our contemporary word
calorie
derives—and the belief at the time was that this fluid heat flowed from areas of high concentration to low, and that caloric could never be either created or destroyed. Joule made note, though, that heat was produced in many ways that suggested it was of a different nature. For example, he studied waterfalls and determined that the water at the bottom was warmer than that at the top, and he concluded that the gravitational potential energy difference between the top and bottom of the waterfall was converted into heat. He also observed that when a paddle wheel was stirring water—a very famous experiment that Joule performed—it raised the temperature of the water, and in 1881 he came up with remarkably accurate
results for the conversion of the kinetic energy of the paddle wheel into heat.
In this experiment Joule connected a set of paddles in a container of water to a pulley and a string from which he suspended a weight. As the weight lowered, the string turned the shaft of the paddles, rotating them in the water container. More technically, he lowered a mass,
m
, on a string over a distance,
h.
The change in potential energy was
mgh
, which the contraption converted into the rotational (kinetic) energy of the paddle, which then heated the water. Here is an illustration of the device:
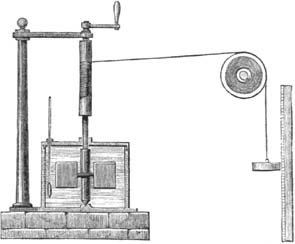
What made the experiment so brilliant is that Joule was able to calculate the exact amount of energy he was transferring to the water—which equaled
mgh.
The weight came down slowly, because the water prevented the paddle from rotating fast. Therefore the weight hit the ground with a negligible amount of kinetic energy. Thus all the available gravitational potential energy was transferred to the water.
How much is a joule? Well, if you drop a 1-kilogram object 0.1 meters (10 centimeters), the kinetic energy of that object has increased by
mgh
, which is about 1 joule. That may not sound like much, but joules can add up quite quickly. In order to throw a baseball just under 100 miles per hour, a Major League Baseball pitcher requires about 140 joules
of energy, which is about the same amount of energy required to lift a bushel of 140 hundred-gram apples 1 full meter.
*
One hundred forty joules of kinetic energy hitting you could be enough to kill you, as long as that energy is released quickly, and in a concentrated fashion. If it were spread out over an hour or two, you wouldn’t even notice it. And if all those joules were released in a pillow hitting you hard, it wouldn’t kill you. But concentrated in a bullet, say, or a rock or a baseball, in a tiny fraction of a second? A very different story.
Which brings us back to wrecking balls. Suppose you had 1,000-kilogram (1-ton) wrecking ball, which you drop over a vertical distance of 5 meters. It will convert about 50,000 joules of potential energy (
mgh
= 1,000 × 10 × 5) into kinetic energy. That’s quite a wallop, especially if it’s released in a very short time. Using the equation for kinetic energy, we can solve for speed too. At the bottom of its swing the ball would be moving at a speed of 10 meters per second (about 22 miles per hour), which is a pretty high speed for a 1-ton ball. To see this kind of energy in action, you can check out an amazing video online of a wrecking ball hitting a minivan that had strayed into a Manhattan construction zone, knocking the van over as though it were a toy car:
www.lionsdenu.com/wrecking-ball-vs-dodge-mini-van/
.
How Much Food Energy Do We Need?
We can come to appreciate the amazing feats of conversion of energy that keep our civilization running by considering the amount of joules involved in the most basic of our life processes. Consider, for example, that in one day a human body generates about 10 million joules of body heat. Unless you’re running a fever, your body runs roughly at a temperature of 98.6 degrees Fahrenheit (37 degrees Celsius), and radiates heat in the form of infrared radiation at the rate, on average, of about 100 joules
per second; very roughly about 10 million joules per day. However, this does depend on air temperature and the size of the human being. The larger the person, the more energy s/he radiates per second. You can compare that to the energy radiated by a lightbulb; 1 watt is equivalent to the expenditure of 1 joule per second, so 100 joules per second equals 100 watts, which means that on average, people radiate at roughly the same level as a 100-watt lightbulb. You don’t feel as hot as a lightbulb because your heat is distributed over a much larger area. When you think that an electric blanket only produces 50 watts, you now understand why, as I’m sure you already know, in winter it’s much nicer to have a human being with you in bed than an electric blanket.
There are dozens of different units for energy: BTUs for air conditioners; kilowatt-hours for electricity; electron volts for atomic physics; ergs for astronomers. A BTU is about 1,055 joules; a kilowatt-hour is the equivalent of 3.6 × 10
6
joules; an electron volt is 1.6 × 10
–19
joules; 1 erg is 10
–7
joules. One very important unit of energy we are all familiar with is the calorie. A calorie is close to 4.2 joules. So, as our bodies generate roughly 10 million joules every day, we are expending a little over 2 million calories. But how can that be? We’re supposed to eat only about 2,000 calories a day. Well, when you read
calorie
on food packages, what the label writers really mean is
kilocalorie
, a thousand calories, sometimes indicated by spelling the word
calorie
with a capital
C
. This is done for convenience, because a single calorie is a very small unit: the amount of energy required to raise the temperature of 1 gram of water 1 degree Celsius. So, in order to radiate 10 million joules per day, you have to eat roughly 2,400 kilocalories (or Calories) of food a day. And if you eat a lot more than that, well, you pay a price sooner or later. The math here is pretty unforgiving, as too many of us know but try to ignore.
