Expanded Universe (41 page)

By 2000 A.D. we will know a great deal about how the brain functions . . . whereas in 1900 what little we knew was wrong.
I do
not
predict that the basic mystery of psychology—how mass arranged in certain complex patterns becomes aware of itself—will be solved by 2000 A.D. I hope so but do not expect it.
9.
1950
Cancer, the common cold, and tooth decay will all be conquered; the revolutionary new problem in medical research will be to accomplish "regeneration," i.e., to enable a man to grow a new leg, rather than fit him with an artificial limb.
1965
In the meantime spectacular progress has been made in organ transplants—and the problem of regeneration is related to this one. Biochemistry and genetics have made a spectacular breakthrough in "cracking the genetic code." It is a tiny crack, however, with a long way to go before we will have the human chromosomes charted and still longer before we will be able to "tailor" human beings by gene manipulation. The possibility is there—but not by year 2000. This is probably just as well. If we aren't bright enough to build decent houses, are we bright enough to play God with the architecture of human beings?
1980
I see no reason to change this prediction if you will let me elaborate (weasel) a little. "The common cold" is a portmanteau expression for upper respiratory infections which appear to be caused by a very large number of different viruses. Viruses are pesky things. It is possible to immunize against them, e.g., vaccination against smallpox, a virus disease. But there are almost no chemotherapies, medicines, against viruses. That is why "the common cold" is treated much the same way today as in 1900, i.e., support the patient with bed rest, liquids, aspirin to make him more comfortable, keep him warm. This was standard in 1900 and it is still standard in 1980.
It is probable that your body makes antibodies against the virus of any cold you catch. But this gives you no protection against that virus's hundreds of close relatives found in any airport, theater, supermarket, or gust of dust off the street. In the meantime, while his kinfolk take turns making you miserable, virus #1 has mutated and you have no antibodies against the mutation.
Good news: Oncology (cancer), immunology, hematology, and "the common cold" turn out to be strongly interrelated subjects; research in all these is moving fast—and a real breakthrough in any one might mean a breakthrough in all.
10.
1950
By the end of this century mankind will have explored this solar system, and the first ship intended to reach the nearest star will be a building.
1965
Our editor suggested that I had been too optimistic on this one—but I still stand by it. It is still thirty-five years to the end of the century. For perspective, look back thirty-five years to 1930—the American Rocket Society had not yet been founded. Another curve, similar to the one herewith in shape but derived entirely from speed of transportation, extrapolates to show faster-than-light travel by year 2000. I guess I'm chicken, for I am not predicting FTL ships by then, if ever. But the prediction still stands without hedging.
1980
My money is still on the table at twenty years and counting. Senator Proxmire can't live forever. In the last 10½ years men have been to the Moon several times; much of the Solar system has been most thoroughly explored within the limits of "black box" technology and more will be visited before this year is out.
Ah, but not explored by
men
—and the distances are so great. Surely they are . . . by free-fall orbits, which is all that we have been using. But there are numerous proposals (and not all ours!) for constant-boost ships, proposals that require R&D on present art only—no breakthroughs.
Reach for your pocket calculator and figure how long it would take to make a trip to Mars and back if your ship could boost at one-tenth gee. We will omit some trivia by making it from parking orbit to parking orbit, use straight-line trajectories, and ignore the Sun's field—we'll be going uphill to Mars, downhill to Earth; what we lose on the roundabouts we win on the shys.
These casual assumptions would cause Dan Alderson, ballistician at Jet Propulsion Laboratory, to faint. But after he comes out of his faint he would agree that our answers would be of correct close order of magnitude—and all I'm trying to prove is that even a slight constant boost makes an enormous difference in touring the Solar System. (Late in the 21st century we'll offer the Economy Tour: Ten Planets in Ten Days.)
There are an unlimited number of distances between rather wide parameters for an Earth-Mars-Earth trip but we will select one that is nearly minimum (it's cheating to wait in orbit at Mars for about a year in order to take the shortest trip each way . . . and unthinkable to wait years for the closest approach). We'll do this Space Patrol style: There's Mars, here we are at L-5; let's scoot over, swing around Mars, and come straight home. Just for drill.
Conditions: Earth-surface gravity (one "gee") is an acceleration of 32.2 feet per second squared, or 980.7 centimeters per second squared. Mars is in or near opposition (Mars is rising as Sun is setting). We will assume that the round trip is 120,000,000 miles. If we were willing to wait for closest approach we could trim that to less than 70,000,000 miles . . . but we might have to wait as long as 17 years. So we'll take a common or garden variety opposition—one every 26 months—for which the distance to Mars is about 50- to 60,000,000 miles and never over 64 million.
(With Mars in conjunction on the far side of the Sun, we could take the scenic route of over 500 million miles—how much over depends on how easily you sunburn. I suggest a minimum of 700 million miles.)
You now have all necessary data to figure the time it takes to travel Earth-Mars-Earth in a constant-boost ship—
any
constant-boost ship—when Mars is at opposition. (If you insist on the scenic route, you can't treat the trajectory approximations as straight lines and you can't treat space as flat but a bit uphill. You'll need Alderson or his equal and a
big
computer, not a pocket calculator; the equations are very hairy and sometimes shoot back.)
But us two space cadets are doing this by eyeballing it, using Tennessee windage, an aerospace almanac, a Mickey Mouse watch, and an SR-50 Pop discarded years ago.
We need just one equation: Velocity equals acceleration times elapsed time: v = at
This tells us that our average speed is ½at—and from that we know that the distance achieved is the average speed times the elapsed time: d = ½at
2
If you don't believe me, check any physics text, encyclopedia, or nineteen other sorts of reference books—and I did that derivation without cracking a book but now I'm going to stop and find out whether I've goofed—I've had years of practice in goofing. (Later—seems okay.)
Just two things to remember: 1) This is a 4-piece trip—boost to midpoint, flip over and boost to brake; then do the same thing coming home. Treat all four legs as being equal or 30,000,000 miles, so figure one of them and multiply by four (Dan, stop frowning; this is an
approximation . . .
done with a Mickey Mouse watch.)
2) You must keep your units straight. If you start with centimeters, you are stuck with centimeters; if you start with feet, you are stuck with feet. So we have ¼ of the trip equals 5280 x 30,000,000 = 1.584 x 10
11
feet, or 4.827 x 10
12
centimeters.
One last bit: Since it is elapsed time we are after, we will rearrange that equation (d = ½at
2
) so that you can get the answer in one operation on your trusty-but-outdated pocket calculator . . . or even on a slide rule, as those four-significant-figures data are mere swank; I've used so many approximations and ignored so many minor variables that I'll be happy to get answers correct to two significant figures.
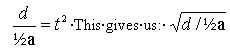
d is 30,000,000 miles expressed in feet, or 158,400,000,000. Set that into your pocket calculator. Divide it by one half of one tenth of gee, or 1.61. Push the square root button. Multiply by 4. You now have the elapsed time of the round trip expressed in seconds so divide by 3600 and you have it in hours, and divide that by 24 and you have it in days.
At this point you are supposed to be astonished and to start looking for the mistake. While you are looking, I'm going to slide out to the refrigerator.
There is no mistake. Work it again, this time in metric. Find a reference book and check the equation. You will find the answer elsewhere in this book but don't look for it yet; we'll try some other trips you may take by 2000 A.D. if you speak Japanese or German—or even English if Proxmire and his ilk fail of reelection.
Same trip, worked the same way, but at only one percent of gee. At that boost I would weigh less than my shoes weigh here in my study.
Hmmph! Looks as if one answer or the other must be wrong.
Bear with me. This time we'll work it at a full gee, the acceleration you experience lying in bed, asleep. (See Einstein's 1905 paper.)
(Preposterous. All three answers must be wrong.)
Please stick with me a little longer. Let's run all three problems for a round trip to Pluto—in 2006 A.D., give or take a year. Why 2006? Because today Pluto has ducked inside the orbit of Neptune and won't reach perihelion until 1989—and I want it to be a bit farther away; I've got a rabbit stashed in the hat.
Pluto ducks outside again in 2003 and by 2006 it will be (give or take a few million miles) 31.6 A.U. from the Sun, figuring an A.U. at 92,900,000 miles or 14,950,000,000,000 centimeters as we'll work this both ways, MKS and English units. (All right, all right—1.495 x 10
13
centimeters; it gets dull here at this typewriter.)
Now work it all three ways, a round trip of 63.2 A.U. at a constant boost of one gravity, one tenth gravity, and one hundredth of a gee—and we'll dedicate this to Clyde Tombaugh, the only living man to discover a new planet—through months of tedious and painstaking examination of many thousands of films.
Some think that Pluto was once a satellite and its small size makes this possible. But it is
not
a satellite today. It is both far too big and hundreds of millions of miles out of position to be an asteroid. It can't be a comet. So it's a planet—or something so exotic as to be still more of a prize.
Its size made it hard to find and thus still more of an achievement. But Tombaugh continued the search for seventeen weary years and many millions more films. If there is an Earth-size planet out there, it is at least three times as distant as Pluto, and a gas giant would have to be six times as far. Negative data win no prizes but they are the bedrock of science.
Until James W. Christy on 22 June 1978 discovered Pluto's satellite, Charon, it was possible for us romantics to entertain the happy thought that Pluto was loaded with valuable heavy metals; the best estimate of its density made this plausible. But the mass of a planet with a satellite can be calculated quite easily and accurately, and from that, its density.
The new figure was much too low, only half again as heavy as water. Methane snow? Perhaps.
So once again a lovely theory is demolished by an awkward fact.
Nevertheless Pluto remains a most mysterious and most intriguing heavenly body. A planet the size and mass of Mars might not be too much use to us out there . . . but think of it as a fuel dump. Many stories and many nonfictional projections speak of using the gas giants and/or the rings of Saturn as sources of fuel. But if Pluto is methane ice or water ice or frozen hydrogen or all three, as a source of fuel—conventional, or fusion, or even reaction mass—Pluto has one supremely important advantage over the gas giants: Pluto is
not
at the bottom of a horridly deep gravity well.
Finished calculating? Good. Please turn to page 299 and see why I wanted our trip to Pluto to be a distance of 31.6 A.U.—plus other goodies, perhaps.
11.
1950
Your personal telephone will be small enough to carry in your handbag. Your house telephone will record messages, answer simple inquiries, and transmit vision.
1965
No new comment.
1980
This prediction is trivial and timid. Most of it has already come true and the telephone system will hand you the rest on a custom basis if you'll pay for it. In the year 2000, with modern telephones tied into home computers (as common then as flush toilets are today) you'll be able to have 3-dimensional holovision along with stereo speech. Arthur C. Clarke says that this will do away with most personal contact in business. I agree with all of Mr. Clarke's arguments and disagree with his conclusion; with us monkey folk there is no substitute for personal contact; we enjoy it and it fills a spiritual need.
Besides that, the business conference is often an excuse to loaf on the boss's time and the business convention often supplies some of the benefits of the Roman Saturnalia.
Nevertheless I look forward to holovideostereophones
without
giving up personal contacts.
