Einstein (51 page)
Authors: Walter Isaacson

The result was not nearly as vivid to the layman as, say,
E=mc
2
. Yet using the condensed notations of tensors, in which sprawling complexities can be compressed into little subscripts, the crux of the final Einstein field equations is compact enough to be emblazoned, as it indeed
often has been, on T-shirts designed for proud physics students. In one of its many variations,
82
it can be written as:
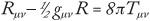
The left side of the equation starts with the term
R
mn
, which is the Ricci tensor he had embraced earlier. The term
g
mn
is the all-important metric tensor, and the term
R
is the trace of the Ricci tensor called the Ricci scalar. Together, this left side of the equation—which is now known as the Einstein tensor and can be written simply as
G
mn
—compresses together all of the information about how the geometry of spacetime is warped and curved by objects.
The right side describes the movement of matter in the gravitational field. The interplay between the two sides shows how objects curve spacetime and how, in turn, this curvature affects the motion of objects. As the physicist John Wheeler has put it, “Matter tells space-time how to curve, and curved space tells matter how to move.”
83
Thus is staged a cosmic tango, as captured by another physicist, Brian Greene:
Space and time become players in the evolving cosmos. They come alive. Matter here causes space to warp there, which causes matter over here to move, which causes space way over there to warp even more, and so on. General relativity provides the choreography for an entwined cosmic dance of space, time, matter, and energy.
84
At last Einstein had equations that were truly covariant and thus a theory that incorporated, at least to his satisfaction, all forms of motion, whether it be inertial, accelerated, rotational, or arbitrary. As he proclaimed in the formal presentation of his theory that he published the following March in the
Annalen der Physik,
“The general laws of nature are to be expressed by equations that hold true for all systems of coordinates, that is they are covariant with respect to any substitutions whatever.”
85
Einstein was thrilled by his success, but at the same time he was worried that Hilbert, who had presented his own version five days earlier in Göttingen, would be accorded some of the credit for the theory. “Only one colleague has really understood it,” he wrote to his friend
Heinrich Zangger, “and he is seeking to nostrify it (Abraham’s expression) in a clever way.” The expression “to nostrify”
(nostrifizieren),
which had been used by the Göttingen-trained mathematical physicist Max Abraham, referred to the practice of nostrification by which German universities converted degrees granted by other universities into degrees of their own. “In my personal experience I have hardly come to know the wretchedness of mankind better.” In a letter to Besso a few days later, he added, “My colleagues are acting hideously in this affair. You will have a good laugh when I tell you about it.”
86
So who actually deserves the primary credit for the final mathematical equations? The Einstein-Hilbert priority issue has generated a small but intense historical debate, some of which seems at times to be driven by passions that go beyond mere scientific curiosity. Hilbert presented a version of his equations in his talk on November 16 and a paper that he dated November 20, before Einstein presented his final equations on November 25. However, a team of Einstein scholars in 1997 found a set of proof pages of Hilbert’s article, on which Hilbert had made revisions that he then sent back to the publisher on December 16. In the original version, Hilbert’s equations differed in a small but important way from Einstein’s final version of the November 25 lecture. They were not actually generally covariant, and he did not include a step that involved contracting the Ricci tensor and putting the resulting trace term, the Ricci scalar, into the equation. Einstein did this in his November 25 lecture. Apparently, Hilbert made a correction in the revised version of his article to match Einstein’s version. His revisions, quite generously, also added the phrase “first introduced by Einstein” when he referred to the gravitational potentials.
Hilbert’s advocates (and Einstein’s detractors) respond with a variety of arguments, including that the page proofs are missing one part and that the trace term at issue was either unnecessary or obvious.
It is fair to say that both men—to some extent independently but each also with knowledge of what the other was doing—derived by November 1915 mathematical equations that gave formal expression to the general theory. Judging from Hilbert’s revisions to his own page proofs, Einstein seems to have published the final version of these equations first. And in the end, even Hilbert gave Einstein credit and priority.
Either way, it was, without question, Einstein’s theory that was being formalized by these equations, one that he had explained to Hilbert during their time together in Göttingen that summer. Even the physicist Kip Thorne, one of those who give Hilbert credit for producing the correct field equations, nonetheless says that Einstein deserves credit for the theory underlying the equations. “Hilbert carried out the last few mathematical steps to its discovery independently and almost simultaneously with Einstein, but Einstein was responsible for essentially everything that preceded these steps,” Thorne notes. “Without Einstein, the general relativistic laws of gravity might not have been discovered until several decades later.”
87
Hilbert, graciously, felt the same way. As he stated clearly in the final published version of his paper, “The differential equations of gravitation that result are, as it seems to me, in agreement with the magnificent theory of general relativity established by Einstein.” Henceforth he would always acknowledge (thus undermining those who would use him to diminish Einstein) that Einstein was the sole author of the theory of relativity.
88
“Every boy in the streets of Göttingen understands more about four-dimensional geometry than Einstein,” he reportedly said. “Yet, in spite of that, Einstein did the work and not the mathematicians.”
89
Indeed, Einstein and Hilbert were soon friendly again. Hilbert wrote in December, just weeks after their dash for the field equations was finished, to say that with his support Einstein had been elected to the Göttingen Academy. After expressing his thanks, Einstein added, “I feel compelled to say something else to you.” He explained:
There has been a certain ill-feeling between us, the cause of which I do not want to analyze. I have struggled against the feeling of bitterness attached to it, with complete success. I think of you again with unmixed geniality and ask you to try to do the same with me. It is a shame when two real fellows who have extricated themselves somewhat from this shabby world do not afford each other mutual pleasure.
90
They resumed their regular correspondence, shared ideas, and plotted to get a job for the astronomer Freundlich. By February Einstein was even visiting Göttingen again and staying at Hilbert’s home.
Einstein’s pride of authorship was understandable. As soon as he got printed copies of his four lectures, he mailed them out to friends. “Be sure you take a good look at them,” he told one. “They are the most valuable discovery of my life.” To another he noted, “The theory is of incomparable beauty.”
91
Einstein, at age 36, had produced one of history’s most imaginative and dramatic revisions of our concepts about the universe. The general theory of relativity was not merely the interpretation of some experimental data or the discovery of a more accurate set of laws. It was a whole new way of regarding reality.
Newton had bequeathed to Einstein a universe in which time had an absolute existence that tick-tocked along independent of objects and observers, and in which space likewise had an absolute existence. Gravity was thought to be a force that masses exerted on one another rather mysteriously across empty space. Within this framework, objects obeyed mechanical laws that had proved remarkably accurate—almost perfect—in explaining everything from the orbits of the planets, to the diffusion of gases, to the jiggling of molecules, to the propagation of sound (though not light) waves.
With his special theory of relativity, Einstein had shown that space and time did not have independent existences, but instead formed a fabric of spacetime. Now, with his general version of the theory, this fabric of spacetime became not merely a container for objects and events. Instead, it had its own dynamics that were determined by, and in turn helped to determine, the motion of objects within it—just as the fabric of a trampoline will curve and ripple as a bowling ball and some billiard balls roll across it, and in turn the dynamic curving and rippling of the trampoline fabric will determine the path of the rolling balls and cause the billiard balls to move toward the bowling ball.
The curving and rippling fabric of spacetime explained gravity, its equivalence to acceleration, and, Einstein asserted, the general relativity of all forms of motion.
92
In the opinion of Paul Dirac, the Nobel laureate pioneer of quantum mechanics, it was “probably the greatest scientific discovery ever made.” Another of the great giants of twentieth-century physics, Max Born, called it “the greatest feat of
human thinking about nature, the most amazing combination of philosophical penetration, physical intuition and mathematical skill.”
93
The entire process had exhausted Einstein but left him elated. His marriage had collapsed and war was ravaging Europe, but Einstein was as happy as he would ever be. “My boldest dreams have now come true,” he exulted to Besso. “
General
covariance. Mercury’s perihelion motion wonderfully precise.” He signed himself “contented but kaput.”
94
DIVORCE
1916–1919

With Elsa, June 1922
As a young man, Einstein had predicted, in a letter to the mother of his first girlfriend, that the joys of science would be a refuge from painful personal emotions. And thus it was. His conquest of general relativity proved easier than finding the formulas for the forces swirling within his family.
Those forces were complex. At the very moment he was finalizing his field equations—the last week of November 1915—his son Hans Albert was telling Michele Besso that he wanted to spend time alone with his father over Christmas, preferably on Zugerberg mountain or someplace similarly isolated. But simultaneously, the boy was writing his father a nasty letter saying he did not want him to come to Switzerland at all.
1
How to explain the contradiction? Hans Albert’s mind seemed at times to display a duality—he was, after all, only 11—and he had powerfully conflicted attitudes toward his father. That was no surprise. Einstein was intense and compelling and at times charismatic. He was also aloof and distracted and had distanced himself, physically and emotionally, from the boy, who was guarded by a doting mother who felt humiliated.
The stubborn patience that Einstein displayed when dealing with scientific problems was equaled by his impatience when dealing with personal entanglements. So he informed the boy he was canceling the trip. “The unkind tone of your letter dismays me very much,” Einstein wrote just days after finishing his last lecture on general relativity. “I see that my visit would bring you little joy, therefore I think it’s wrong to sit in a train for two hours and 20 minutes.”
There was also the question of a Christmas present. Hans Albert had become an avid little skier, and Mari gave him a set of equipment that cost 70 francs. “Mama bought them for me on condition that you also contribute,” he wrote. “I consider them a Christmas present.” This did not please Einstein. He replied that he would send him a gift in cash, “but I do think
gave him a set of equipment that cost 70 francs. “Mama bought them for me on condition that you also contribute,” he wrote. “I consider them a Christmas present.” This did not please Einstein. He replied that he would send him a gift in cash, “but I do think
that a luxury gift costing 70 francs does not match our modest circumstances,
” Einstein wrote, underlining the phrase.
2
