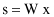Data Mining (16 page)
Authors: Mehmed Kantardzic

This analysis shows that X is a candidate for reduction because its mean values are close and, therefore, the final test is below the threshold value. On the other hand, the test for feature Y is significantly above the threshold value; this feature is not a candidate for reduction because it has the potential to be a distinguishing feature between two classes.
A similar idea for feature ranking is shown in the algorithm that is based on correlation criteria. Let us consider first the prediction of a continuous outcome
y
. The Pearson correlation coefficient is defined as:

where
cov
designates the covariance and
var
the variance. The estimate of
R
(
i
) for the given data set with samples’ inputs
x
k,,j
and outputs
y
k
is defined by:
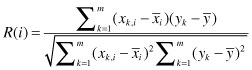
where the bar notation stands for an average over the index
k
(set of all samples). Using
R
(
i
)
2
as a variable-ranking criterion enforces a ranking according to goodness of linear fit of individual variables. Correlation criteria such as
R
(
i
)
2
can only detect linear dependencies between input features and target or output feature (variable). One common criticism of variable ranking is that it leads to the selection of a redundant subset. The same performance could possibly be achieved with a smaller subset of complementary variables. Still, one may wonder whether deleting presumably redundant variables can result in a performance gain.
Practical experiments show that noise reduction and consequently better model estimation may be obtained by adding features that are presumably redundant. Therefore, we have to be very careful in the preprocessing analysis. Yes, perfectly correlated variables are truly redundant in the sense that no additional information is gained by adding them. But, even variables with relatively high correlation (or anti-correlation) do not guarantee absence of variables’ complementarity. We can find cases where a feature looks completely useless by itself, and it is ranked very low, but it can provide significant information to the model and performance improvement when taken with others. These features by themselves may have little correlation with the output, target concept, but when combined with some other features, they can be strongly correlated with the target feature. Unintentional removal of these features can result in poor mining performance.
The previous simple methods test features separately. Several features may be useful when considered separately, but they may be redundant in their predictive ability. If the features are examined collectively, instead of independently, additional information can be obtained about their characteristics and mutual relations. Assuming normal distributions of values, it is possible to describe an efficient technique for selecting subsets of features. Two descriptors characterize a multivariate normal distribution:
1.
M, a vector of the m feature means, and
2.
C, an m × m covariance matrix of the means, where C
i,i
are simply the variance of feature i, and C
i,j
terms are correlations between each pair of features
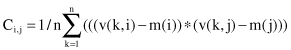
where
v(k,i) and v(k,j) are the values of features indexed with i and j,
m(i) and m(j) are feature means, and
n is the number of dimensions.
These two descriptors, M and C, provide a basis for detecting redundancies in a set of features. If two classes exist in a data set, then the heuristic measure, DM, for filtering features that separate the two classes is defined as
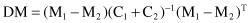
where M
1
and C
1
are descriptors of samples for the first class, and M
2
and C
2
for the second class. Given the target of k best features, all subsets of k from m features must be evaluated to find the subset with the largest DM. With large data sets that have large numbers of features, this can be a huge search space, and alternative heuristic methods should be considered. One of these methods selects and ranks features based on an entropy measure. Detailed explanations are given in Section 3.4. The other heuristic approach, explained in the following, is based on a combined correlation and covariance analyses and ranking of all features.
Existing efficient feature-selection algorithms usually rank features under the assumption of feature independence. Under this framework, features are ranked as relevant mainly based on their individual high correlations with the output feature. Because of the irreducible nature of feature interactions, these algorithms cannot select interacting features. In principle, it can be shown that a feature is relevant due to two reasons: (1) It is strongly correlated with the target feature, or (2) it forms a feature subset and the subset is strongly correlated with the target. A heuristic approach is developed to analyze features of type (2) in the selection process.
In the first part of a selection process, the features are ranked in descending order based on their correlation values with output using a previously defined technique. We may assume that a set of features S can be divided into subset S1 including relevant features, and subset S2 containing irrelevant ones. Heuristically, critical for removal are features in S2 first, while features in S1 are more likely to remain in the final set of selected features.
In the second part, features are evaluated one by one starting from the end of the S2 ranked feature list. The monotonic property suggests that the backward elimination search strategy fits best in feature selection. That is, one can start with the full feature set and successively eliminate features one at a time from the bottom of the ranked list if their interaction does not contribute to better correlation with output. The criterion could be, for example, based on a covariance matrix. If a feature, together with previously selected features, shows influence on the output with less than threshold value (it could be expressed through some covariance matrix factor), the feature is removed; otherwise it is selected. Backward elimination allows every feature to be evaluated with the features it may interact with. The algorithm repeats until all features in the S2 list are checked.
3.2.2 Feature Extraction
The art of data mining starts with the design of appropriate data representations. Better performance is often achieved using features derived from the original input. Building a feature representation is an opportunity to incorporate domain knowledge into the data and can be very application-specific. Transforming the input set into a new, reduced set of features is called
feature extraction
. If the features extracted are carefully chosen, it is expected that the new feature set will extract the relevant information from the input data in order to perform the desired data-mining task using this reduced representation.
Feature-transformation techniques aim to reduce the dimensionality of data to a small number of dimensions that are linear or nonlinear combinations of the original dimensions. Therefore, we distinguish two major types of dimension-reduction methods: linear and nonlinear. Linear techniques result in
k
new derived features instead of initial p (k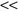 p). Components of the new feature are a linear combination of the original features:
p). Components of the new feature are a linear combination of the original features:
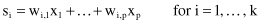
or in a matrix form