Chances Are (31 page)
Authors: Michael Kaplan

The deeper difficulty is that legal probability is a function of opinion: our view of the truth of a conclusion, based on our view of the truth of some evidence. Classical probability is about things; legal probability is about thought. What legal reasoning required was a calculus of
personal
probability: a method to track the trajectory of opinion as it passed through the gravitational fields of new and unexpected facts.
personal
probability: a method to track the trajectory of opinion as it passed through the gravitational fields of new and unexpected facts.
Â
The solution appeared in 1763 among the papers of a recently deceased Presbyterian minister in the quiet English spa town of Tunbridge Wells. The Reverend Thomas Bayes was a Fellow of the Royal Society and accounted a good amateur mathematician, but he had made little name for himself during his lifetime. He left his papers to a long-neglected friend, Richard Price, who found in them what he considered excellent ammunition against the skeptical views of David Hume. Hume, you will remember, said that the fact the sun has risen every morning gives us no evidence about the likelihood of its rising tomorrow.
An Essay Towards Solving a Problem in the Doctrine of Chances,
the piece Price found in Bayes' papers, offered precisely this: a method to measure confidence in the probability of a single event based on the experience of many.
An Essay Towards Solving a Problem in the Doctrine of Chances,
the piece Price found in Bayes' papers, offered precisely this: a method to measure confidence in the probability of a single event based on the experience of many.
Bayes'
Essay
occupies in probability circles much the same position as
Das Kapital
in economics or
Finnegans Wake
in literature: everyone refers to it and no one reads it. What is now called Bayes' theorem uses modern notation and is most easily demonstrated with a diagram. Say you want to know the probability of an event
A given
the occurrence of another event
B:
what is described in modern notation as
P
(
A
|
B
).
Essay
occupies in probability circles much the same position as
Das Kapital
in economics or
Finnegans Wake
in literature: everyone refers to it and no one reads it. What is now called Bayes' theorem uses modern notation and is most easily demonstrated with a diagram. Say you want to know the probability of an event
A given
the occurrence of another event
B:
what is described in modern notation as
P
(
A
|
B
).
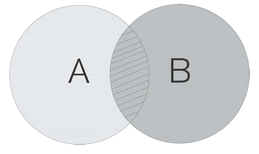
Looking at the diagram, we can see that the probability of
both
events happeningâ
P
(
AB
)âis the shared area in the middle; moreover,
P
(
AB
) is the same as
P
(
BA
): it is Saturday and sunny, sunny and Saturday. We can also see that the probability of both events happening given that B
has
happenedâthe “conditional” probabilityâis shown by the proportion of
AB
to all of
B
. Rewriting this sentence as an equation gives us:
both
events happeningâ
P
(
AB
)âis the shared area in the middle; moreover,
P
(
AB
) is the same as
P
(
BA
): it is Saturday and sunny, sunny and Saturday. We can also see that the probability of both events happening given that B
has
happenedâthe “conditional” probabilityâis shown by the proportion of
AB
to all of
B
. Rewriting this sentence as an equation gives us:
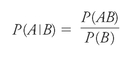
We are now ready for a little manipulation. As is always the case in algebra, almost anything is allowed as long as we do it to both sides of an equation. We'll start with our two ways of describing the center section of the diagram:
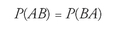
We then multiply both sides of that equation by 1âbut, sneakily, we'll use slightly different ways of expressing 1 for each.
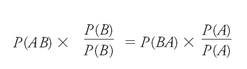
which is the same as:
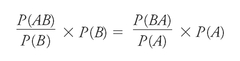
But wait! The first term on each side is also our definition of conditional probability; so, by substitution, we produce:
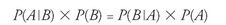 and, dividing both sides by
and, dividing both sides by
P
(
B
), we get:
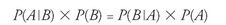
P
(
B
), we get:
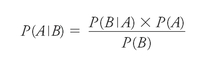
Where are we going with this? As is so often the case, we seem deepest into arbitrary juggling of terms when we are actually closest to a surprising truth. There is one last feat to accomplish, though. Look back at
B
in the diagram. We could, humorously, define it as the sum of its parts: as being everything that is
both B
and
A
âthat is,
P
(
BA
)âplus everything that is
B
and
not A
:
P
(
BA
). With two passes of our trusty definition of conditional probability, we could then expand this to say:
B
in the diagram. We could, humorously, define it as the sum of its parts: as being everything that is
both B
and
A
âthat is,
P
(
BA
)âplus everything that is
B
and
not A
:
P
(
BA
). With two passes of our trusty definition of conditional probability, we could then expand this to say:
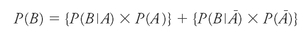
In more straightforward terms, this tells us that the overall chance of
B
happening is a weighted combination of its probability
given
that
A
happens (times
A
's own probability), and its probability given that
not
-
A
happens (times not-
A
's own probability). Casanova's chance of seducing the countess depends on how swayed she is by charm
times
the likelihood that he will be charming
plus
how repelled she is by boorishness
times
the chance that he will be a boor.
B
happening is a weighted combination of its probability
given
that
A
happens (times
A
's own probability), and its probability given that
not
-
A
happens (times not-
A
's own probability). Casanova's chance of seducing the countess depends on how swayed she is by charm
times
the likelihood that he will be charming
plus
how repelled she is by boorishness
times
the chance that he will be a boor.
Let's slot this expanded version of
P
(
B
) into our equation in progress:
P
(
B
) into our equation in progress:
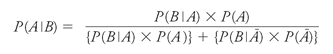
Or:
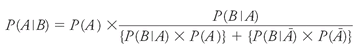
Other books
Deep Surrendering (Episode Two) by Cameron, Chelsea M.
Mr. Monk and the New Lieutenant by Hy Conrad
Transhuman by Mark L. Van Name, T. K. F. Weisskopf
Full Disclosure by Sean Michael
The Sentinel by Jeffrey Konvitz
Scat by Carl Hiaasen
Cold-Hearted by Christy Rose
Roots by Alex Haley
Baby V (Chianti Kisses #1) by Tara Oakes
