Chances Are (16 page)
Authors: Michael Kaplan

Bernoulli's was an appropriate worry for a century that was making the seismic shift from science as a chain of logical deductions based on principle, to science as a body of conclusions based on observation. Pascal's
a priori
vision of chance was, like his theology, axiomatic, eternal, true before and after any phenomenaâand therefore ultimately sterile. Even in the most rule-constrained situations in real life, however, knowing the rules is rarely enough.
a priori
vision of chance was, like his theology, axiomatic, eternal, true before and after any phenomenaâand therefore ultimately sterile. Even in the most rule-constrained situations in real life, however, knowing the rules is rarely enough.
Clearly, probability needed a way to work with the facts, not just the rules: to make sense of things as and
after
they happen. To believe that truth simply arises through repeated observation is to fall into a difficulty so old that its earliest statement was bequeathed by Heraclitus to the temple of Artemis at Ephesus more than two thousand years ago: “You cannot step into the same river twice.” Life is flow, life is change; the fact that something has occurred cannot itself guarantee that it will happen again. As the Scottish skeptic David Hume insisted, the sun's having risen every day until now makes no difference whatever to the question of whether it will rise tomorrow; nature simply does not operate on the principle of “what I tell you three times is true.”
after
they happen. To believe that truth simply arises through repeated observation is to fall into a difficulty so old that its earliest statement was bequeathed by Heraclitus to the temple of Artemis at Ephesus more than two thousand years ago: “You cannot step into the same river twice.” Life is flow, life is change; the fact that something has occurred cannot itself guarantee that it will happen again. As the Scottish skeptic David Hume insisted, the sun's having risen every day until now makes no difference whatever to the question of whether it will rise tomorrow; nature simply does not operate on the principle of “what I tell you three times is true.”
Rules, however beautiful, do not allow us to conclude from facts; observation, however meticulous, does not in itself ensure truth. So are we at a dead end? Bernoulli's
Ars Conjectandi
â
The Art of Hypothesizing
âsets up arrows toward a way out. His first point was that for any given phenomenon, our uncertainty about it decreases as the number of our observations of it increases.
Ars Conjectandi
â
The Art of Hypothesizing
âsets up arrows toward a way out. His first point was that for any given phenomenon, our uncertainty about it decreases as the number of our observations of it increases.
This is actually more subtle than it appears. Bernoulli noticed that the more observations we make, the less likely it is that
any one of them
would be the exact thing we are looking for: shoot a thousand times at a bull's-eye, and you greatly increase the number of shots that are near but not in it. What repeated observation actually does is
refine our opinion,
offering readings that fall within progressively smaller and smaller ranges of error: If you meet five people at random, the proportion of the sexes cannot be more even than 3 to 2, a 10 percent margin of error; meet a thousand and you can reduce your expected error to, say, 490 to 510: a 0.1 percent margin.
any one of them
would be the exact thing we are looking for: shoot a thousand times at a bull's-eye, and you greatly increase the number of shots that are near but not in it. What repeated observation actually does is
refine our opinion,
offering readings that fall within progressively smaller and smaller ranges of error: If you meet five people at random, the proportion of the sexes cannot be more even than 3 to 2, a 10 percent margin of error; meet a thousand and you can reduce your expected error to, say, 490 to 510: a 0.1 percent margin.
As so often happens in mathematics, a convenient re-statement of a problem brings us suddenly up against the deepest questions of knowledge. Instinctively, we want to know what the answerâthe ratio, the likelihoodâ
really
is. But no matter how carefully we set up our experiment, we know that repeated observation never reveals absolute truth. If, however, we change the problem from “What is it really?” to “How wrong about it can I bear to be?”âfrom God's truth to our own fallibilityâBernoulli has the answer. Here it is:
really
is. But no matter how carefully we set up our experiment, we know that repeated observation never reveals absolute truth. If, however, we change the problem from “What is it really?” to “How wrong about it can I bear to be?”âfrom God's truth to our own fallibilityâBernoulli has the answer. Here it is:
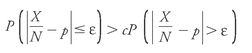
This formula, like all others, is a kind of bouillon cube, the result of intense, progressive evaporation of a larger, diffuse mix of thought. Like the cube, it can be very usefulâbut it isn't intended to be consumed raw. You want to determine an unknown proportion
p:
say, the proportion of the number of houses that actually burn down in a given year to the total number of houses. This law says that you can specify a number of observations,
N
, for which the likelihood
P
that the difference between the proportion you observe (
X
houses known to have burned down out of
N
houses counted:
X/N
) and
p
will be
within
an arbitrary degree of accuracy, ε, is more than
c
times greater than the likelihood that the difference will be
outside
that degree of accuracy. The
c
can be a number as large as you like.
p:
say, the proportion of the number of houses that actually burn down in a given year to the total number of houses. This law says that you can specify a number of observations,
N
, for which the likelihood
P
that the difference between the proportion you observe (
X
houses known to have burned down out of
N
houses counted:
X/N
) and
p
will be
within
an arbitrary degree of accuracy, ε, is more than
c
times greater than the likelihood that the difference will be
outside
that degree of accuracy. The
c
can be a number as large as you like.
Â
Â
This is the Weak Law of Large Numbersâthe basis for all our dealings with repeated phenomena of uncertain causeâand it states that for
any
given degree of accuracy, there is a finite number of observations necessary to achieve that degree of accuracy. Moreover, there is a method for determining how many further observations would be necessary to achieve 10, or 100, or 1,000 times that degree of accuracy. Absolute certainty can never be achieved, though; the aim is what Bernoulli called “moral certainty”âin essence, being as sure of this as you can be of anything.
any
given degree of accuracy, there is a finite number of observations necessary to achieve that degree of accuracy. Moreover, there is a method for determining how many further observations would be necessary to achieve 10, or 100, or 1,000 times that degree of accuracy. Absolute certainty can never be achieved, though; the aim is what Bernoulli called “moral certainty”âin essence, being as sure of this as you can be of anything.
Bernoulli was a contemporary of Newton and, like him, worked on the foundations of calculus. One might say Bernoulli's approach to deriving “moral certainty” from multiple examples looks something like the notion of “limit” in calculus: if, for example, you want to know the slope of a smooth curve at a given pointâwell, you can't. What you
can
do is begin with the slope of a straight line between that point and another nearby point on the curve and then observe how the slope changes as you move the nearby point toward the original point. You achieve any desired degree of accuracy by moving your second point sufficiently close to your first.
can
do is begin with the slope of a straight line between that point and another nearby point on the curve and then observe how the slope changes as you move the nearby point toward the original point. You achieve any desired degree of accuracy by moving your second point sufficiently close to your first.
It wasn't just the
fact
that moral certainty could be achieved that interested Bernoulli; he wanted to know
how many
cases were necessary to achieve a given degree of certaintyâand his law offers a solution.
fact
that moral certainty could be achieved that interested Bernoulli; he wanted to know
how many
cases were necessary to achieve a given degree of certaintyâand his law offers a solution.
As so often in the land of probability, we are faced with an urn containing a great many white and black balls, in the ratio (though we don't know it) of 3 black to 2 white. We are in 1700, so we can imagine a slightly dumpy turned pearwood urn with mannerist dragon handles, the balls respectively holly and walnut. How many times must we draw from that urn, replacing the ball each time, to be willing to guess the ratio between black and white? Maybe a hundred times? But we still might not be very sure of our guess. How many times would we have to draw to be 99.9 precent sure of the ratio? Bernoulli's answer, for something seemingly so intangible, is remarkably precise: 25,550. 99.99 percent certain? 31,258. 99.999 percent? 36,966. Not only is it possible to attain “moral certainty” within a finite number of drawn balls, but each order of magnitude of greater certainty requires fewer and fewer extra draws. So if you are seventy years (or, rather, 25,550 days) old, you can be morally certain the sun will rise tomorrowâwhatever David Hume may say.
This discovery had two equally important but opposite implications, depending in part on whether you think 25,550 is a small or large number. If it seems small, then you will see how the justification for gathering mass data was now fully established. Until Bernoulli's theorem, there was no reason to consider that looking closely at death lists or tax receipts or how many houses burn in London was other than idle curiosity, as there was no proof that frequent observations could be more valid than ingenious assumptions. Now, though, there was the Grail of moral certaintyâthe promise that enough observations could make one 99.9 percent sure of conjectures that the finest wits could not have teased from first principles. If 25,550 seems large to you, however, then you will have a glimpse of the vast prairies of scientific drudgery that the Weak Law of Large Numbers brought under its dominion. The law is a devourer of data; it must be fed to produce its certainties. Think how many poor scriveners, inspectors, census-takers, and graduate students have given the marrow of their lives to preparing consistent series of facts to serve this tyrannical theorem: mass fact, even before mass production, made man a machine. And the data, too, must be standardized, for if any two observations in the series are not directly comparable, the term
X/N
in the formula has no meaning. The Law collapses, and we are back bantering absolute truth with Aristotle and Hume. The fact that we now have moral certainty of so many scientific assertions is a monument to the humility and patience, not just the genius, of our forebears.
X/N
in the formula has no meaning. The Law collapses, and we are back bantering absolute truth with Aristotle and Hume. The fact that we now have moral certainty of so many scientific assertions is a monument to the humility and patience, not just the genius, of our forebears.
Â
Genius, though, must have its place; every path through probability must stop for a moment to recognize another aspect of the genius of Laplace. His work binds together the
a priori
rules of frequency developed by Pascal and the
a posteriori
observations foreshadowed by Bernoulli into a single, consistent discipline: a calculus of probabilities, based on ten Principles. But Laplace did not stop at unifying the theory: he took it further, determining not just how likely a predetermined matter like a coin toss might be, nor how certain we can be of something based on observationâbut how we ought to
act
upon that degree of certainty or uncertainty.
a priori
rules of frequency developed by Pascal and the
a posteriori
observations foreshadowed by Bernoulli into a single, consistent discipline: a calculus of probabilities, based on ten Principles. But Laplace did not stop at unifying the theory: he took it further, determining not just how likely a predetermined matter like a coin toss might be, nor how certain we can be of something based on observationâbut how we ought to
act
upon that degree of certainty or uncertainty.
His own career in public office ended disastrously after only six weeks (“He brought into the administration,” complained Napoleon, “the spirit of the infinitesimals”), but Laplace retained a strong interest in the moral and political value of his work: “The most important questions of life . . . are indeed for the most part only problems of probability.” His 5th Principle, for instance, determines the absolute probability of an expected event linked to an observed one (such as, say, the likelihood of tossing heads with a loaded coin, given the observed disproportion of heads to tails in past throws). In explaining it, Laplace moved quickly from the standard example of coin tossing to shrewd and practical advice: “Thus in the conduct of life constant happiness is a proof of competency which should induce us to employ preferably happy persons.”
Laplace's calculus brought order to insurance in his lecture “Concerning Hope,” where he introduced a vital element that had previously been missing from the formal theory of chance: the natural human desire that things should come out one way rather than another. It added a new layerâwhat Laplace called “mathematical hope”âto the question of probability: an event had not only a given likelihood but a value, for good or ill, to the observer. The way these two layers interact was described in three Principlesâand one conclusionâthat are worth examining in detail.
8th Principle:
When the advantage depends on several events it is obtained by taking the sum of the products of the probability of each event by the benefit attached to its occurrence.
When the advantage depends on several events it is obtained by taking the sum of the products of the probability of each event by the benefit attached to its occurrence.
Â
This is the gambling principle you will remember from Chapter 4: If the casino offers you two chips if you flip heads on the first attempt and four chips if you flip heads
only
on the second attempt, you should multiply each chance of winning by its potential gains and then add them together: (1/2 Ã 2) + (1/4 Ã 4) = 2. This means, if it costs
fewer
than two chips to play, you should take the chance. If the price is moreâwell, then you know you're in a real casino.
only
on the second attempt, you should multiply each chance of winning by its potential gains and then add them together: (1/2 Ã 2) + (1/4 Ã 4) = 2. This means, if it costs
fewer
than two chips to play, you should take the chance. If the price is moreâwell, then you know you're in a real casino.
Of course, the same arithmetic applies to losses as it does to gains: mathematical fear is just the inverse of mathematical hope. So, if you felt you had a 1-in-2 chance of losing $2 million and a 1-in-4 chance of losing $4 million, you would happily (or at least willingly) pay a total premium of up to $2 million to insure against your whole potential loss. It is this ability to bundle individual chances into one overall risk that makes it possible to insure large enterprises.
Â
9th Principle:
In a series of probable events of which the ones produce a benefit and the others a loss, we shall have the advantage which results from it by making a sum of the products of the probability of each favorable event by the benefit it procures, and subtracting from this sum that of the products of the probability of each unfavorable event by the loss which is attached to it. If the second sum is greater than the first, the benefit becomes a loss and hope is changed to fear.
In a series of probable events of which the ones produce a benefit and the others a loss, we shall have the advantage which results from it by making a sum of the products of the probability of each favorable event by the benefit it procures, and subtracting from this sum that of the products of the probability of each unfavorable event by the loss which is attached to it. If the second sum is greater than the first, the benefit becomes a loss and hope is changed to fear.
Now this really does begin to sound like real life, where not everything that happens is a simple bet on coin flipsâand where good and bad fortune are never conveniently segregated. Few sequences of events are pleasure unalloyed: every Christmas present has its thank-you letter. So how do we decide whether, on balance, this course is a better choice than that? Laplace says here that probability, like addition, doesn't care about orderâjust as you know that 1 - 3 + 2 - 4 will give you the same result as 1 + 2 - 3 - 4, you can comb out any tangled skein of probable events into positive and negative (based on their individual likelihood multiplied by their potential for gain or loss) and then add each column up and compare the sums, revealing whether you should face this complex future with joy or despair.
This method, too, is an essential component of insurance, particularly insuring credit. Whether a given person or company is a good or bad credit risk involves just this sort of winnowing of favorable from unfavorable aspects and gauging the probability of each. “The good news is he drives a Rolls-Royce; the bad news is he doesn't own it.” As the recent spectacular failures among large corporations reveal, it's a process that requires a fine hand on the calculator. This is something we will see again and again: each time probability leaves its cozy study full of urns and dice and descends to the marketplace of human affairs, it reveals its dependence on human capabilitiesâon judgment and definition. As powerful a device as it is, it remains a hand tool, not a machine.
Other books
Elvis and the Tropical Double Trouble by Webb, Peggy
Oppression by Therrien, Jessica
The Secret (Dr Steven Dunbar 10) by McClure, Ken
Maverick Sheriff by Delores Fossen
UpAndComing by Christi Ann
Claws and Effect by Rita Mae Brown
Always You by Jill Gregory
Girlfriend in a coma by Douglas Coupland
Fixed Up by Maddie Jane
The Setup by Marie Ferrarella
