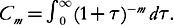Birth of a Theorem: A Mathematical Adventure (24 page)
Read Birth of a Theorem: A Mathematical Adventure Online
Authors: Cédric Villani
Tags: #Non-Fiction, #Science, #Biography

(7.25)
where
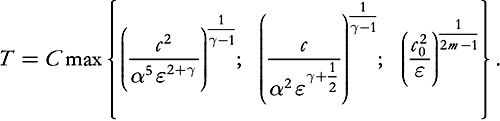
(7.26)
(ii) Assume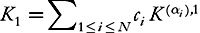 for some
for some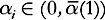 , where
, where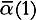 appears in Proposition 7.1; then there is a numeric constant
appears in Proposition 7.1; then there is a numeric constant
Γ
>
0
such that whenever
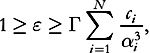
one has, with the same notation as in (i),
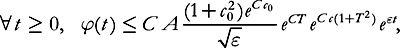
(7.27)
where
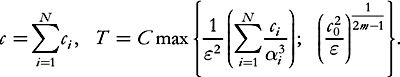
Proof of Theorem 7.7.
We only treat (i), since the reasoning for (ii) is rather similar; and we only establish the conclusion as an
a priori
estimate, skipping the continuity/approximation argument needed to turn it into a rigorous estimate. Then the proof is done in three steps.
Step 1:
Crude pointwise bounds.
From (7.22) we have
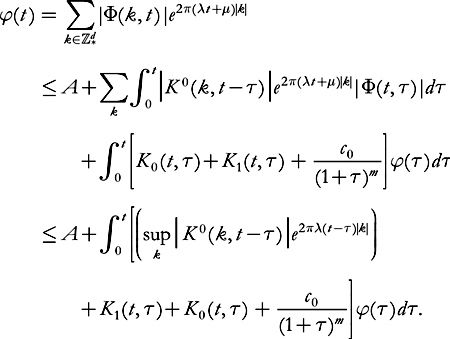
(7.28)
We note that for any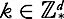 and
and
t
≥
0,
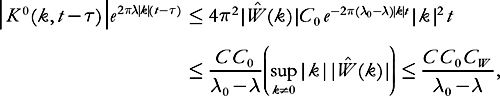
where (here as below)
C
stands for a numeric constant which may change from line to line. Assuming
∫
K
0
(
t,
τ
)
d
τ
≤
1/2, we deduce from (7.28)
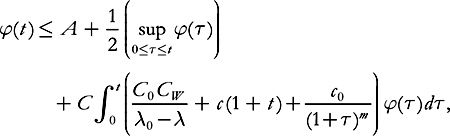
and by Gronwall’s lemma
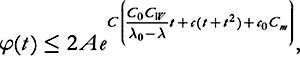
(7.29)
where