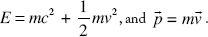Beyond the God Particle (50 page)
Read Beyond the God Particle Online
Authors: Leon M. Lederman,Christopher T. Hill
Tags: #Science, #Cosmology, #History, #Physics, #Nuclear, #General

4
. In relativity we find the energy and momentum of the moving particle
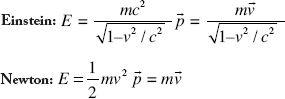
where we have written the Newtonian expressions for comparison. We can see the “Newtonian limit” and the nonzero rest energy implied for zero velocity,
v
= 0, where the Einstein formulas go into
In special relativity, we can never get the speed of a massive particle (one with nonzero inertial mass
m
) to equal the speed of light. As the momentum and the energy become infinite. It therefore would require an infinite energy to accelerate a proton to the speed of light. E = mc
the momentum and the energy become infinite. It therefore would require an infinite energy to accelerate a proton to the speed of light. E = mc
2
holds strictly for a particle at rest.
At the CERN LHC at full design energy we accelerate protons to seven trillion electron volts. The rest mass energy of a proton is about one billion electron volts. Hence, the LHC “boosts” a proton to have a “Lorentz factor”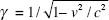 of about 7,000. This means that approximately (v/c)
of about 7,000. This means that approximately (v/c)
2
= 0.99999998, or that the LHC accelerates protons to 99.999999 percent of the speed of light.
How, then, can anything travel at the speed of light? We see that if we take and also allow our particle to be massless, then the energy is actually indeterminate, that is, we get,
and also allow our particle to be massless, then the energy is actually indeterminate, that is, we get,
E
= 0/0. However, this allows for the possibility that a massless particle, something with no inertial mass, can have finite energy and momentum. If we look at the relationship between energy and momentum, we see that a massless particle must satisfy: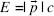 . Indeed, this describes the particles of light, the photons. Photons have absolutely no inertial mass, yet they carry energy and momentum as they travel through space. Photons travel forever at the speed of light. They cannot be at rest, or have a finite velocity less than
. Indeed, this describes the particles of light, the photons. Photons have absolutely no inertial mass, yet they carry energy and momentum as they travel through space. Photons travel forever at the speed of light. They cannot be at rest, or have a finite velocity less than
c
, for then their energy would be zero.
5
. For a short yet poignant biography of Emmy Noether, see
chapter 3
of
Symmetry and the Beautiful Universe
by Lederman and Hill. Also, the “conservation of energy” and its relationship to the “constancy of the laws of physics in time” are explained by the amusing example of the “ACME Power Company” in
chapter 2
.
CHAPTER 5. MASS UNDER THE MICROSCOPE
1
. To measure the mass of a water molecule, we start by looking up the mass of 1 mole of hydrogen, which is listed on the Periodic Table of the Elements as about 1 gram. A mole of oxygen is listed as 16 grams. Therefore, an H
2
O molecule has 18 grams per mole. A “mole” is a definite number of particles, about 6 × 10
23
particles. This is “Avogadro's number,” and determining this number makes the basic connection between aggregate matter and the number of atoms per unit mass comprising it (we're rounding things to one significant digit). So the mass of a single H
2
O molecule is 18 grams/ (6 × 10
23
), or 3 × 10
–23
grams, hence 3 × 10
–26
kilograms.
In this way, with more care, we can measure the mass of the proton, the neutron, and—with more effort—even the lowly electron, as well as masses of all sorts of atomic and subatomic things. We often quote these masses as an energy, using Einstein's E = mc
2
. We did this earlier for the electron (about 0.5 million electron volts, or MeV, of mass in equivalent energy units) and our celebrant, the muon (about 105 MeV).
Sometimes you'll see a mass quoted in MeV/c
2
, or GeV/c
2
, which rewrites Einstein's formula as m = E/c
2
and installs the factor of /c
2
. Most physicists simply use units in which c = 1 and Planck's constant h-bar = h/2
π
= 1, and then use electron volts, eV, as the measure of mass, distance, and time. For example, 1 GeV (Giga electron volts) corresponds to (0.2 × 10
–13
cm)
–1
.
2
. See “Galaxy,”
http://en.wikipedia.org/wiki/Galaxy
(site last visited 4/1/2013).
3
. See chapter 1,
note 13
; see also “Superconductivity,”
http://en.wikipedia.org/wiki/Superconductivity
, “Ginzburg–Landau Theory,”
http://en.wikipedia.org/wiki/Ginzburg%E2%80%93Landau_theory
, “John Bardeen,”
http://en.wikipedia.org/wiki/John_Bardeen
, “Leon Cooper,”
http://en.wikipedia.org/wiki/Leon_Cooper
, “Robert Schrieffer,”
http://en.wikipedia.org/wiki/Robert_Schrieffer
, “V. Ginzburg,”
http://en.wikipedia.org/wiki/Vitaly_Lazarevich_Ginzburg
, “Lev Landau”
http://en.wikipedia.org/wiki/Lev_Landau
(sites last visited 4/1/2013).
In a superconductor the vibrations of the lattice of atoms that make up the material interact with the electrons. This interaction is very delicate, but at ultra-cold temperatures, it causes the electrons to pair up, forming little particles that are like “two-electron atoms” and that behave quite differently than unpaired electrons. These are called Cooper pairs, and they form a kind of quantum soup inside of the superconductor. This quantum soup is the structure of the vacuum itself, the state of lowest energy, inside of a superconductor. When a photon then enters the superconductor it interacts with the soup. This causes the photon to blend with the soup and behave exactly like a photon that has a mass. The massive photon can be brought to rest in the superconductor, but in fact it is really the original massless photon and soup combination that is brought to rest.
4
. See “Jeffrey Goldstone,”
http://en.wikipedia.org/wiki/Jeffrey_Goldstone
, “Giovanni Jona-Lasinio,”
http://en.wikipedia.org/wiki/Giovanni_Jona-Lasinio
, “Yoichiro Nambu,”
http://en.wikipedia.org/wiki/Yoichiro_Nambu
(sites last visited 4/2/2013).
5
. This is a quantum phenomenon. The rapid flip-flop between L and R chiralities is associated with a rapid oscillating behavior of the muon at rest. This was first realized when people considered the resting state solutions to Dirac's equation that described quantum states of electrons, muons, etc. in a manner consistent with relativity. It was given a fancy German name: “Zitterbewegung.”
One might be worried that the L-R-L-R oscillation involves a rapid change in momentum from east to west, back to east, etc. For a localized particle, one at rest, this rapid fluctuation in momentum can be viewed as consistent with Heisenberg's uncertainty principle, Δp Δx
. The “point-like” resting massive particle can be viewed as localized to within Δx = h/2
π
mc (the “Compton wavelength”) and can therefore fluctuate in momentum by Δp = mc.
CHAPTER 6. THE WEAK INTERACTIONS AND THE HIGGS BOSON
1
. Leon Lederman, Melvin Schwartz, and Jack Steinberger received the Nobel Prize in Physics in 1988 for their research that revealed the “flavors” of neutrinos. The neutrinos are paired with corresponding charged leptons. There are therefore three charged leptons: electron, muon, and tau, and three associated neutrinos: