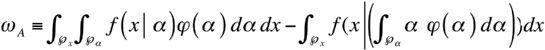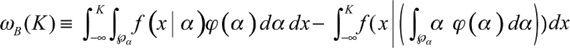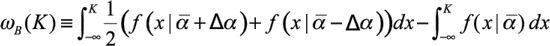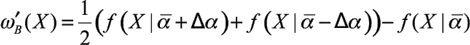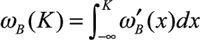Antifragile: Things That Gain from Disorder (84 page)
Read Antifragile: Things That Gain from Disorder Online
Authors: Nassim Nicholas Taleb

If the price of wine in the international markets rises by, say, 40 percent, then there are clear benefits. But should the price drop by an equal percentage, −40 percent, then massive harm would ensue, in magnitude larger than the benefits should there be an equal rise. There are concavities to the exposure—severe concavities.
And clearly, should the price drop by 90 percent, the effect would be disastrous. Just imagine what would happen to your household should you get an instant and unpredicted 40 percent pay cut. Indeed, we have had problems in history with countries specializing in some goods, commodities, and crops that happen to be not just volatile, but extremely volatile. And disaster does not necessarily come from variation in price, but problems in production: suddenly, you can’t produce the crop because of a germ, bad weather, or some other hindrance.
A bad crop, such as the one that caused the Irish potato famine in the decade around 1850, caused the death of a million and the emigration of a million more (Ireland’s entire population at the time of this writing is only about six million, if one includes the northern part). It is very hard to reconvert resources—unlike the case in the doctor-typist story, countries don’t have the ability to change. Indeed, monoculture (focus on a single crop) has turned out to be lethal in history—one bad crop leads to devastating famines.
The other part missed in the doctor-secretary analogy is that countries don’t have family and friends. A doctor has a support community, a circle of friends, a collective that takes care of him, a father-in-law to borrow from in the event that he needs to reconvert into some other profession, a state above him to help. Countries don’t. Further, a doctor has savings; countries tend to be borrowers.
So here again we have fragility to second-order effects.
Probability Matching:
The idea of comparative advantage has an analog in probability: if you sample from an urn (with replacement) and get a black ball 60 percent of the time, and a white one the remaining 40 percent, the optimal strategy, according to textbooks, is to bet 100 percent of the time on black. The strategy of betting 60 percent of the time on black and 40 percent on white is called “probability matching” and considered to be an error in the decision-science literature (which I remind the reader is what was used by Triffat in
Chapter 10
). People’s instinct to engage in probability matching appears to be sound, not a mistake. In nature, probabilities are unstable (or unknown), and probability matching is similar to redundancy, as a buffer. So if the probabilities change, in other words if there is another layer of randomness, then the optimal strategy is probability matching.
How specialization works:
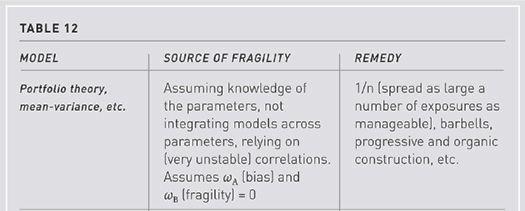
The reader should not interpret what I am saying to mean that specialization is not a good thing—only that one should establish such specialization after addressing fragility and second-order effects. Now I do believe that Ricardo is ultimately right, but not from the models shown. Organically, systems without top-down controls would specialize progressively, slowly, and over a long time, through trial and error, get the right amount of specialization—not through some bureaucrat using a model. To repeat, systems make small errors, design makes large ones.
So the imposition of Ricardo’s insight-turned-model by some social planner would lead to a blowup; letting tinkering work slowly would lead to efficiency—true efficiency. The role of policy makers should be to,
via negativa
style, allow the emergence of specialization by preventing what hinders the process.
Model second-order effects and fragility:
Assume we have the right model (which is a very generous assumption) but are uncertain about the parameters. As a generalization of the deficit/employment example used in the previous section, say we are using
f,
a simple function:
f
(
x
|
ᾱ
), where
ᾱ
is supposed to be the average expected
input variable, where we take
φ
as the distribution of
α
over its domain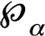 ,
,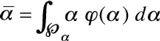 .
.
The philosopher’s stone
: The mere fact that
α
is uncertain (since it is estimated) might lead to a bias if we perturbate from the
inside
(of the integral), i.e., stochasticize the parameter deemed fixed. Accordingly, the convexity bias is easily measured as the difference between (a) the function
f
integrated across values of potential
α,
and (b)
f
estimated for a single value of
α
deemed to be its average. The convexity bias (philosopher’s stone)
ω
A
becomes:
1
The central equation:
Fragility is a partial philosopher’s stone below
K,
hence
ω
B
the missed fragility is assessed by comparing the two integrals below
K
in order to capture the effect on the left tail:
which can be approximated by an interpolated estimate obtained with two values of
α
separated from a midpoint by ∆
α
its mean deviation of
α
and estimating
Note that antifragility
ω
C
is integrating from
K
to infinity. We can probe
ω
B
by point estimates of
f
at a level of
X
≤
K
so that
which leads us to the fragility detection heuristic (Taleb, Canetti, et al., 2012). In particular, if we assume that
ω
´
B
(
X
) has a constant sign for
X
≤
K
, then
ω
B
(
K
) has the same sign. The detection heuristic is a perturbation in the tails to probe fragility, by checking the function
ω
´
B
(
X
) at any level
X
.