Alex’s Adventures in Numberland (78 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

The
continued fraction
is a strange type of fraction constructed by an infinite process of additions and divisions.
Whe
n phi is expressed as a continued fraction it looks like this:
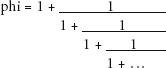
To understand how this works, let’s take the fraction line by line and see that it closes in on phi:
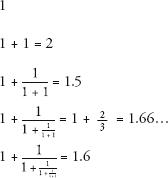
And so on.
Continued fractions provide mathematicians with a way of rating how irrational a number might be. Since the expression for phi contains only 1s, it is the ‘purest’ continued fraction that there is, and hence is considered the ‘most irrational’ number.
During the writing of this book there were four tomes that were always on my desk, and whose contribution cannot be isolated to any individual chapter. Martin Gardner remains peerless in p
opular maths for his erudition, wit and clarity. Tobias Dantzig’s
Number
is a classic about the cultural evolution of mathematics. Both the Ifrah and the Cajori are painstakingly well researched and endlessly fascinating.
Cajori, F.,
A History of Mathematical Notations
, Dover, 1993 (facsimile of original by Open Court, Illinois, 1928/9)
Dantzig, T.,
Number
, Plume, New York, 2007 (originally Macmillan, 1930)
Gardner, M.,
Mathematical Games: The Entire Collection of His Scientific American Columns
, Mathematical Association of America, 2005
Ifrah, G.,
The Universal History of Numbers
, John Wiley, New York, 2000
CHAPTER ZERO
This chapter is based on conversations in London with Brian Butterworth, and in Paris with Stanislas Dehaene and Pierre Pica. At University College London I was screened for dyscalculia by Teresa Iuculano and Marinella Cappelletti, with a computer program now used in schools in the UK. I’m not dyscalculic, which is probably no great surprise. If you would like to help support the Munduruku’s protection of their traditional education and environment, donations can be sent to: The Munduruku Fund, The Arrow Rainforest Foundation, 5 Southridge Place, London SW20 8JQ, United Kingdom. More details can be found on: www.thearrowrainforestfoundation.com
Butterworth, B.,
The Mathematical Brain
, Macmillan, London, 1999
Dehaene, S.,
The Number Sense
, Oxford University Press, Oxford, 1997
Matzusawa, T. (ed.),
Primate Origins of Human Cognition and Behavior
, Springer, Tokyo, 2001
Angier, N., ‘Gut Instinct’s Surprising Role in Math’,
New York Times
, 2008
Dehaene, S., Izard, V., Spelke, E., and Pica, P., ‘Log or Linear?’,
Science
, 2008
Inoue, S., and Matsuzawa, T., ‘Working memory of numerals in chimpanzees’,
Current Biology
, 2007
Pica, P., Lerner, C., Izard, V., and Dehaene, S., ‘Exact and Appropriate Arithmetic in an Amazonian Indigene Group’,
Science
, 2004
Siegler, R.S., and Booth, J.L., ‘Development of Numerical Estimation in Young Children’,
Child Development
, 2004
CHAPTER ONE
Anyone wanting more information about the joys of base 12 can reach the Dozenal Society of America at [email protected], or 5106 Hampton Avenue Suite 205, Saint Louis, Missouri 63109-3115, USA.
Little Twelvetoes
is a classic of
Schoolhouse Rock!
, a series of musical cartoons about maths, science and grammar from the 1970s that can all be seen on the internet. My entry into the abacus world was only made possible by Kouzi Suzuki, a one-man
soroban
evangelist, who met me at a Tokyo rail station dressed up as Sherlock Holmes.
Andrews, F.E.,
New Numbers
, Faber & Faber, London, 1936
Duodecimal Society of America, Inc.,
Manual of the Dozen System
, Duodecimal Society of America, New York, 1960
Elbrow, Rear-Admiral G.,
The New English System of Money, Weights and Measures and of Arithmetic
, P.S. King & Son, London, 1913
Essig, J.,
Douze, notre dix future
, Dunod, Paris, 1955
Glaser, A.,
History of Binary and Other Nondecimal Numeration
, Southampton, PA, 1971
Kawall Leal Ferreira, M. (ed.),
Idéias Matemáticas de Povos Culturalmente Distintos
, Global Editora, São Paulo, 2000
Suzuki, K.,
Lectures on Soroban
, Institute for English Yomiagezan
Dowker, A., and Lloyd D., ‘Linguistic influences on numeracy’,
Education Transactions
, University of Bangor, 2005
Wassmann, J., and Dasen, P.R., ‘Yupno Number System and Counting’,
Cross-cultural Psychology Journal
, 1994
Hammarström, H., ‘Rarities in Numeral Systems’, 2007
CHAPTER TWO
Proofs Without Words
is a gem, and was my source for the different Pythagoras proofs. Thanks to Tom Hull for much of the background about origami. The illustrations of how to make business-card tetrahedrons and cubes are inspired by his book. Another remarkable Japanese religio-geometric practice is
sangaku
, which didn’t fit in the chapter but is too fascinating not to mention here. A
sangaku
is a wooden tablet hung at a Buddhist or Shinto shrine that has a proof of a geometric prlem painted on it. Between the seventeenth and nineteenth centuries, thousands of
sangaku
were made by Japanese who had worked out geometrical problems but could not afford to publish them in books. Drawing the solutions on a tablet and hanging them at a shrine was a way of making a religious offering while also advertising their results.
Shortly before going to press, I learnt that Jerome Carter had died in a motorcycle accident in 2009.
Balliett, L.D.,
The Philosophy of Numbers
, L.N. Fowler, 1908
Bell, E.T.,
Numerology
, Century, 1933
Dudley, U.,
Numerology
, Mathematical Association of America, 1997
du Sautoy, M.,
Finding Moonshine
, Fourth Estate, London, 2008
Ferguson, K.,
The Music of Pythagoras
, Walker, New York, 2008
Hull, T.,
Project Origami
, A.K. Peters, Wellesley, MA, 2006
Kahn, C.H.,
Pythagoras and the Pythagoreans, a Brief History
, Hackett, Indianapolis, IN, 2001
Loomis, E.S.,
The Pythagorean Proposition
, Edwards Bros, Ann Arbor, MI, 1940
Maor, E.,
The Pythagorean Theorem
, Princeton University Press, NJ, 2007
Mlodinow, L.,
Euclid’s Window
, Free Press, New York, 2001
Nelsen, R.B.,
Proofs Without Words
, Mathematical Association of America, Washington DC, 1993
Riedwig, C.,
Pythagoras, His Life, Teaching and Influence
, Cornell University Press, Ithaca, NY, 2002
Schimmel, A.,
The Mystery of Numbers
, Oxford University Press, New York, 1993
Simoons, F.J.,
Plants of Life, Plants of Death
, University of Wisconsin Press, Madison, WI, 1998
Sundara Rao, T.,
Geometric Exercises in Paper Folding
, Open Court, Chicago, IL, 1901
Bolton, N.J., and MacLeod, D.N.G., ‘The Geometry of the Sri Yantra’,
Religion
, vol. 7, 1977
Burnyeat, M.F., ‘Other Lives’,
London Review of Books
, 2007
CHAPTER THREE
Even though the
Liber Abaci
was first published in 1202, its first English translation did not appear until its 800th anniversary, in 2002. Vedic mathematics is not the only type of speed arithmetic in the market. There are several ‘systems’ and many of them share the same tricks. The best known is the Trachtenberg System, devised by Jakow Trachtenberg while a political prisoner in a Nazi concentration camp. Self-styled ‘mathemagician’ Arthur Benjamin is an entertaining, recent purveyor of the speed arithmetician’s art.
Fibonacci, L.,
Fibonacci’s Liber Abaci
, Springer, New York, 2002
Joseph, G.G.,
Crest of the Peacock
, Penguin, London, 1992
Knott, K.,
Hinduism: A Very Short Introduction
, Oxford University Press, 1998
Seife, C.,
Zero
, Souvenir Press, London, 2000
Tirthaji, Jagadguru Swami S. B. K.,
Vedic Mathematics
, Motilal Banarsidass, Delhi, 1992
Dani, S.G., ‘Myths and reality: On “Vedic mathematics”’
CHAPTER FOUR
The least dweeby contestant in Leipzig was Rüdiger Gamm, a former bodybuilder who failed maths at school. After a career with exaggeratedly large biceps, he now has an exaggeratedly large brain. Gamm, whose calculation skills have made him a minor celebrity in Germany, told me that memory is his greatest asset: ‘I think I have [stored] 200,000 to 300,000 numbers in my head.’
(I found this chapter a challenge because of having to restrain myself from the temptation to make terrible puns about pi. Mathematicians have a congenital propensity to overpun. When we see a word we can’t help but break it down and rearrange it, which probably also explains why the world’s top Scrabble players are maths and computer-science graduates, not linguists.)
Arndt, J., and Haenel, C.,
Pi Unleashed
, Springer, London, 2002
Beckmann, P.,
A History of Pi
, St Martin’s Press, New York, 1971
Berggren L., Borwein J., and Borwein P.,
Pi: A Source Book
, Springer, London, 2003
Bidder, G.,
A short Account of George Bidder, the celebrated Mental Calculator: with a Variety of the most difficult Questions, Proposed to him at the principal Towns in the Kingdom, and his surprising rapid Answers!
, W.C. Pollard, 1821
Colburn, Z.,
A memoir of Zerah Colburn, written by himself
, G. & C. Merriam, Springfield, MA, 1833
Rademacher, H., and Torplitz, O.,
The Enjoyment of Mathematics
, Princeton University Press, NJ, 1957
Aitken, A.C., ‘The Art of Mental Calculation; with Demonstrations’,
Society of Engineers Journal and Transactions
, 1954
Preston, R., ‘The Mountains of Pi’,
New Yorker
, 1992
CHAPTER FIVE
Acheson, D.,
1089 and all that
, Oxford University Press, Oxford, 2002
Berlinski, D.,
Infinite Ascent
, The Modern Library, New York, 2005
Dale, R.,
The Sinclair Story
, Duckworth, London, 1985
Derbyshire, J.,
Unknown Quantity
, Atlantic Books, London, 2006
Hopp, P.M.,
Slide Rules, Their History, Models and Makers
, Astragal Press, New Jersey, 1999
Maor, E.,
e: The Story of a Number
, Princeton University Press, NJ, 1994
Rade, L., and Kaufman, B.A.,
Adventures with Your Pocket Calculator
, Pelican, London, 1980
Schlossberg, E., and Brockman, J.,
The Pocket Calculator Game Book
, William Morrow, New York, 1975
Vine, J.,
Fun & Games with Your Electronic Calculator
, Babani Press, London, 1977 (published in the US as
Boggle
, Price, Stern, Sloane Publishers, Los Angeles, CA, 1975)
CHAPTER SIX
The
Mother Goose/Liber Abaci
sequence of powers of seven also appears in modified form in Islamic folklore: the Angel of Mohammed is said to have 70,000 heads, each of which has 70,000 faces, each with 70,000 mouths, each with 70,000 tongues, each speaking 70,000 languages. Which makes a grand total of about 1.7 million billion billion languages.
I found Dudeney’s articles in
Strand Magazine
brilliantly well written, irrespective of the genius of the puzzles, and well worth a read. I am grateful to Angela Newing, the world expert on Henry Dudeney, for some of the biographical details, and to Jerry Slocum, for solving all my other puzzles about puzzles. If anyone wants an ambigram tattoo, check out Mark Palmer’s creations at www.wowtattoos.com.
Bachet, C.G.,
Amusing and Entertaining Problems that can be Had with Numbers
(
very useful for inquisitive people of all kinds who use arithmetic
), Paris, 1612
Bodycombe, D.J.,
The Riddles of the Sphinx
, Penguin, London, 2007
Danesi, M.,
The Puzzle Instinct
, University of Indiana Press, Indianapolis, IN, 2002
Elffers, J., and Schuyt, M.,
Tangram
, 1997
Gardner, M.,
Mathematics, Magic and Mystery
, Dover, New York, 1956
Hardy, G.H.,
A Mathematician’s Apology
, Cambridge University Press, Cambridge, 1940
