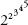Alex’s Adventures in Numberland (47 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

Not one to sit idly by, Neil Sloane took up the chase and uncovered a second:
*
24547284284866560000000000
Sloane is now confident that there are no other indestructible digits.
Consider that for a moment: Conway’s powertrain is such a lethal machine that it annihilates every number in the universe apart from 2592 and 24547284284866560000000000 – two seemingly unrelated, fixed points in the never-ending expanse of numbers. ‘The result is spectacular,’ said Sloane. Big numbers die frly quickly under the powertrain calculation for the same reason that they do under persistence – a zero appears and the whole thing reduces to naught. I asked Sloane if the robustness of the two numbers to survive the powertrain might have any application in the real world. He didn’t think so. ‘It is just amusing. Nothing wrong with that. You have to have fun.’
And Sloane does have fun. He has studied so many sequences that he’s developed his own number aesthetics. One of his favourite sequences was devised by the Colombian mathematician Bernardo Recamán Santos, called the Recamán sequence:
(A5132) 0, 1, 3, 6, 2, 7, 13, 20, 12, 21, 11, 22, 10, 23, 9, 24, 8, 25, 43, 62, 42, 63, 41, 18, 42, 17, 43, 16, 44, 15, 45…
Look at the numbers and try to see a pattern. Follow them carefully. They jump around neurotically. It’s all messed up: one up here, one down there, one over there.
In fact, though, the numbers are generated using the following simple rule: ‘subtract if you can, otherwise add’. To get the
n
th term, we take the
previous
term and either add or subtract
n
from it. The rule is that subtraction must be used
unless
that results in either a negative number or in a number that is already in the sequence. Here’s how the first eight terms are calculated.

And so on.
This rather plodding process takes the integers and calculates answers that look totally haphazard. But a way to see the pattern that emerges is to plot the sequence as a graph, as shown below. The horizontal axis is the position of the terms, so the
n
th term is at
n
, and the vertical axis is the value of the terms. The graph of the first thousand terms of the Recamán sequence is probably unlike any other graph you have seen. It is like the spray of a garden sprinkler, or a child trying to join up dots. (The thick lines in the graph are clumps of dots, since the scale is so big.) ‘It is interesting to see how much order you can bring into chaos,’ Sloane remarked. ‘The Recamán sequence is right on the borderline between chaos and beautiful maths and that’s why it is so fascinating.’
The clash between order and disorder in the Recamán sequence can also be appreciated musically. The
Encyclopedia
has a function that allows you to listen to any sequence as musical notes. Imagine a piano keyboard with 88 keys, which comprise a spread of just under eight octaves. The number 1 makes the piano play its lowest note, the number 2 makes it play the second-lowest note, and so on all the way up to 88, which commands the highest note. When the notes run out, you start at the bottom again, so 89 is back to the first key. The natural numbers 1, 2, 3, 4, 5…sound like a rising scale set on an endless loop. The music created by the Recamán sequence, however, is chilling. It sounds like the soundtrack of a horror movie. It is dissonant, but it does not sound random. You can hear noticeable patterns, as if there is a human hand mysteriously present behind the cacophony.
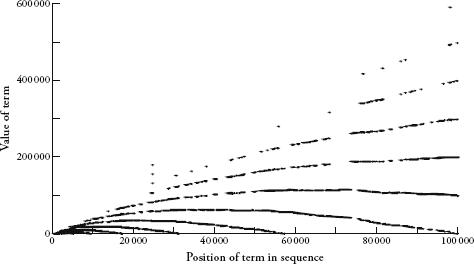
The Recamán sequence.
The question that interests mathematicians about Recamán is whether the sequence contains every number. After 10
25
terms of the sequence the smallest missing number is 852,655. Sloane suspects that every number will eventually appear, including 852,655, but this remains unproved. It’s not hard to understand why Sloane finds Recamán so compelling.
Another favourite of Sloane’s is Gijswijt’s sequence,
*
because, unlike many sequences that grow gloriously fast, Gijswijt’s increases at a mind-bogglingly dawdling pace. It’s a wonderful metaphor for never giv
ing up:
(A90822) 1, 1, 2, 1, 1, 2, 2, 2, 3, 1, 1, 2, 1, 1, 2, 2, 2, 3, 2, 1, 1, 2…
The first time that a 3 appears is in the ninth position. A 4 appears for the first time in the 221st position. You would search until hell almost freezes over for the first time 5 rears its head, which occurs at about position 10100000000000000000000000.
This is an extremely large number. By comparison, the universe contains only 10
80
elementary particles. Eventually, 6 pops up too, at a distance so far away that its position can only be conveniently described as a power of a power of a power of power:
The other numbers will also eventually appear, although – it must be stressed – with no sense of urgency. ‘The land is dying, even the oceans are dying,’ said Sloane with poetic flourish, ‘but one can take refuge in the abstract beauty of sequences like Dion Gijswijt’s A090822.’
As well as paying serious attention to prime numbers, the Greeks were even more enthralled by what they called
perfect
numbers. Consider the number 6: the numbers that divide it – its
factors
– are 1, 2 and 3. If you add 1, 2 and 3,
voilà
, you get 6 again. A perfect number is any number, like 6, that is equal to the sum of its factors. (Strictly speaking, 6 is also a factor of 6, but in discussions of perfection it only makes sense to include the factors of a number
less
than the given number.) After six, the next perfect number is 28 because the numbers that divide it are 1, 2, 4, 7 and 14, the sum of which is 28. Not only the Greeks, but Jews and Christians too attached cosmological significance to such numerical perfection. The ninth-century Benedictine theologian Rabanus Maurus wrote, ‘Six is not perfect because God has created the world in 6 days; rather, God has perfected the world in 6 days because the number was perfect.’
The practice of adding the factors of a number leads to the most whimsical concepts in maths. Two numbers are
amicable
if the sum of the factors of the first number equals the second number, and if the sum of the factors of the second number equals the first. For example, the factors of 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110. Added they equal 284. The factors of 284 are 1, 2, 4, 71 and 142. Together they make 220. Sweet! The Pythagoreans saw 220 and 284 as symbols of friendship. During the Middle Ages talismans with these numbers were made, to promote love. One Arab wrote that he tried to test the erotic effect of eatg something labelled with the number 284, while a partner was eating something labelled 220. It was only in 1636 that Pierre de Fermat discovered the second set of amicable numbers: 17,296 and 18,416. Because of the advent of computer processing, more than 11 million amicable pairs are now known. The largest pair has more than 24,000 digits each, which makes them tricky to write on a slice of baklava.
In 1918 the French mathematician Paul Poulet coined the term
sociable
for a new type of numerical friendship. The five numbers listed below are sociable because if you add up the factors of the first one, you get the second. If you add up the factors of the second, you get the third. If you add up the factors of the third, you get the fourth, the factors of the fourth give you the fifth, and the factors of the fifth get you back to where you started: they add up to the first:
12,496
14,288
15,472
14,536
14,264
Poulet discovered only two chains of sociable numbers – the five numbers above and a less exclusive gang of 28 numbers beginning with 14,316. The next set of sociable numbers was discovered by Henri Cohen, but not until 1969. He found nine sociable chains of just four numbers each, of which the chain with the lowest values is 1,264,460, 1,547,860, 1,727,636 and 1,305,184. Currently, 175 chains of sociable numbers are known, and almost all are chains of four numbers. None are chains of three (particularly poetic, since we all know that three’s a crowd, and a group of four is much more sociable). The longest chain remains Poulet’s 28, which is curious, as 28 is also a perfect number.
It was the Greeks who worked out an unexpected link between perfect numbers and prime numbers, which led to many further numerical adventures. Consider the sequence of doubles starting at 1:
(A79) 1, 2, 4, 8, 16…
In
The Elements
, Euclid showed that whenever the sum of doubles is a prime number, then you can create a perfect number by multiplying the sum by the highest double that you added. This sounds like a mouthful, so let’s start adding doubles to see what he means:
1 + 2 = 3. 3 is prime, so, we multiply 3 with the highest double, which is 2. 3 × 2 = 6, and 6 is a perfect number.
1 + 2 + 4 = 7. Again, 7 is prime. So we multiply 7 by 4 to get another perfect number: 28.
1 + 2 + 4 + 8 = 15. This is not prime. No perfect numbers here.
1 + 2 + 4 + 8 + 16 = 31. This is prime, and 31×16 = 496, which is perfect.
1 + 2 + 4 + 8 + 16 + 32 = 63. This is not prime.
1 + 2 + 4 + 8 + 16 + 32 + 64 = 127. This is prime and 127×64 = 8, which is perfect.
1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 = 255. This is not prime.
Euclid’s proof was, of course, done through geometry. He did not write it out in terms of numbers, instead using line segments. If he’d had the luxury of modern algebraic notation, he would have noticed that he could express the sum of doubles 1 + 2 + 4 +…as the sum of powers of two, 2
0
+ 2
1
+ 2
2
+…(Any number to the power 0 is always 1, by convention, and any number to the power 1 is itself.) It then becomes clear that any sum of doubles is equal to the next-largest double minus 1. For example:
1 + 2 = 3 = 4 – 1
or
20
+ 2
1
= 2
2
– 1
1 + 2 + 4 = 7 = 8 – 1