A Step Farther Out (24 page)

The spacecraft weigh about a metric ton (1000 kilograms or 2200 pounds) and are accelerated at 30 g's for about 30 seconds; that puts them in orbit. While the capsule is in the atmosphere the laser is pulsed at about 250 hertz (cycles per second when I was in school). Each pulse causes the air in the receiving chamber to expand and be expelled rapidly. The chamber refills and another pulse hits: a laser-powered ramjet. For the final kick outside the atmosphere the laser power is absorbed directly in the chamber and part of the spacecraft itself is ablated off and blown aft to function as reaction mass. Of the 1000 kg. start-weight, about 900 kg. goes into orbit.
Some 80 metric tons can be put into orbit each hour at a total cost of around 3000 megawatt-hours. Figuring electricity at 3¢ a kilowatt hour, that's $150 thousand, less than a dollar a kilogram for fuel costs. Obviously there are operating costs and the spacecraft aren't free, but the whole system is an order of magnitude more economical than anything we have now.
Conventional power plants cost something like $300 a kilowatt; a 3000 megawatt power plant would run close to a billion dollars in construction costs. However, when it isn't being used for space launches it could feed power into the national grid, so some of that is recovered as salable power. The laser installation might easily run $5 billion, and another $5 billion in research may be needed.
The point is that for an investment on the order of what we put out to go to the Moon, we could buy the research and construct the equipment for a complete operating spaceflight system, and then begin to exploit the economic possibilities of cheap spaceflight.
There are a lot of benefits to an economical system for getting into orbit. Some are commercial, things like materials that can only be made in gravity-free environments and such like. Others are not precisely commercial, but highly beneficial. For example, the power/pollution problem is enormously helped. Solar cells can collect sunlight that would have fallen onto the Earth. They convert it to electricity and send it down from orbit by microwave. That's fed into the power grid, and when it's used it becomes heat that would have arrived here anyway; the planetary heat balance isn't affected.
Interestingly enough, it's now believed that orbiting solar power plants can be economically competitive with conventional plants, provided that we get the cost of a pound in orbit down to about $20. The laser-launch system could power itself.
We don't even have to build a permanent power plant to get the laser-launcher into operation. There are a lot of old rocket motors around, and they're very efficient at producing hot ionized gasses. Hot ionized gas is the power source for electricity extracted by magneto-hydro-dynamics, or MHD. MHD is outside the scope of this article, but basically a hot gas is fed down a tube wrapped with conducting coils, and electricity comes out. MHD systems are about as efficient as turbine systems for converting fuel to electricity, and they can burn hydrogen to reduce pollution.
The rocket engines wouldn't last forever, and it takes power to make the hydrogen they'd burn—but we don't have to use the system forever. It needn't last longer than it takes to get the big station built in space and start up a solar-screen power plant.
None of this is fantasy. The numbers work. Avco has done some experiments with small-scale laser powered "rockets," and they fly. There are no requirements for fundamental breakthroughs, only a lot of development engineering, to get a full-scale working system.
__________
__________
Laser-launchers are in about the stage that rockets were in, say, 1953. Fifteen years and less than $20 billion would do the job: we'd have a system to get nearly anything we wanted into orbit.
That doesn't seem like very much to get halfway to anywhere.
__________
Those Pesky Belters and Their Torchships
*Quibblers will know that you'd have to stay in the plane of the ecliptic or use a lot more energy to get out of it; and that the Galaxy itself has a very high escape velocity, in the order of 100 km/sec from here. . .
The other day I got a phone call from a national magazine, and being basically kind, generous, and always in need of an excuse to stop working, I spent an hour with the reporter. He wanted a list of ten science fiction predictions that have proved out, and ten more SF writers have made but which haven't happened yet.
He wasn't at all interested in a list of science fiction predictions that just aren't going to happen. Except in rare moods neither am I, but I've just finished reading the death-knell for poly-water (it turns out poly-water isn't a new form of water at all; it's just a product of dirty laboratory glassware) and that plus the phone call got me thinking about nice ideas that just won't work no matter what we do.
One of our favorite SF themes is the "Belter Civilization," which usually seeks—and gets—independence from the colonial masters on Earth. Belters make their livings as asteroid miners, and they flit from asteroid to asteroid, slicing up planetoids for the rich veins of metal we'll presumably find in them.
In the usual story, the miners go off on long prospecting tours, leaving their families on a "settled" rock. The Belt Capital is usually located on Ceres or some other central place which may or may not have been extensively transformed; and when Belters get together, it's always in an asteroid city.
The Belters don't ever come to Earth or any other planet. Indeed, they regard planets as "holes," deep gravity wells which can trap them and use up their precious fuels. The assumption here is that it's far less costly to flit from asteroid to asteroid than it is to land on a planet or get into close orbit around one.
Another assumption, generally not stated in the stories, is that fuels are expensive and scarce, and the Belters have to conserve reaction mass; this is why, in the usual Belter story, you conserve both time and energy by never going outside the Belt. Scarce as fuel is, though, I suppose the Belters have a source of it locally or they couldn't contemplate independence. They must have fuel for their ships and energy for their artificial environments. Without those, there'd be no Belter Civilization. Even if we discover something of fabulous value in the Belt we can't operate without energy and fuel.
Those are not, by the way, the same thing. Nuclear fission reactors and large solar panels could provide enough power for a permanent Belt station, and if there were something valuable enough out there we could put a reactor onto an asteroid now. Rocket fuels are something else again. To make a rocket work, you must have reaction mass: something to get moving fast backwards and dump overboard. Unfortunately, asteroids are rock, and rocks don't make very good rocket fuel. We'll come back to what the Belters might do about that later.
For the moment, let's see how difficult travel to and in the Belt is. We'll use the same measure as last time, the total change in ship velocity required to perform the mission. This is called delta v, and you should recall that a ship with a given fuel efficiency and ratio of fuel to non-fuel weight will have a unique calculatable delta v. It doesn't matter whether the pilot uses that delta v in little increments or in one big burn: the sum of velocity changes remains the same.
Similarly, various mission delta-v requirements can be calculated from the laws of orbital mechanics independent of the ship used. Figure 14 gives the delta-v requirements for getting around the Earth-Jupiter portion of the solar system. We're assuming that getting to Earth orbit is free, whether with the laser launching system I described previously, or with shuttles, or whatever, so all missions to or from Earth begin and end in orbit.
The first thing we see is that landing on an asteroid isn't much easier than going to Mars; in fact, Ceres is harder to get to than Mars. This is because not only are the asteroids a long way out, but they don't help you catch up to them; they've so little mass that you have to chase them down. Thus, once among the asteroids, you may well want to stay there and not use up all that delta v coming back to Earth.
Then, too, travel between Ceres and a theoretical asteroid 2 AU out is a lot cheaper than getting to Earth from either of them. (One AU, or astronomical unit, is the distance from Earth to the Sun and is 93,000,000 miles, or 149,500,000 = 1.5 x 10
8
kilometers.) It takes 8 km/sec to get to the 2 AU rock, but only 3.2 more to get from there to Ceres.
So far so good, and we're well on the way to developing a Belt Civilization. There's already a small nit to pick, though: although travel to Mars itself is costly, it's as easy to get to Mars
orbit
as it is to go from asteroid to asteroid. Thus, if a laser-launch system could be built on Mars, making travel to and from Mars orbit cheap, Mars might well become the Belt Capital.
Politics being what they are, though, perhaps the Martians (well, Mars colonists?) won't like having all those crude asteroid miners on their planet, and the Belters will have to build their own capital at some convenient place such as Ceres or the 2 AU rock, saving both their feelings and some energy. However, we've so far said nothing about how
long
it takes to get from one place to another. The delta v's in Figure 14 are for minimum energy trips, Hohmann transfer orbits, and to use a Hohmann orbit you must start and finish with origin and destination precisely opposite the Sun. You can't just boom out when you feel like it; you must wait for the precise geometry, otherwise the delta-v requirements go up to ridiculous values.
You get a launch window once each synodic period. A synodic period is the time it takes two planets, or planetoids, to go around the sun and come back to precisely the same positions relative to each other: from, say, being on opposite sides of the Sun until they're in opposition again, which is what we need for a Hohmann journey.
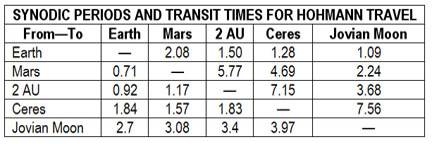
The synodic periods and travel times are given in Figure 15, and our Belt Civilization is in trouble again. Not only does it take 1.57 years to get from Ceres to 2 AU (or vice versa), but you can only do it once each 7 years! Travel to and from Mars isn't a lot better, either. The Belters aren't going to visit their Capital very often, and one wonders if a civilization can be built among colonies that can only visit each other every seven to nine years, spending years in travel times to do it.
By contrast, you can get from Earth to the flying rocks every year and a half, spending another year-and-a-half in transit. That's no short time either, but it beats the nine years of the Ceres-asteroid visitations.
Perhaps, though, we haven't been quite fair to the Belters. Asteroids aren't as widely separated as Ceres and our 2 AU rock Most textbooks claim the asteroids are concentrated between 2.1 and 3.3 AU out from the Sun. We'll assume they're all in the same plane (they aren't), so the Belt area works out to 4.6 x 10
27
square centimeters. The books say there are about 100,000 asteroids visible with the Palomar Eye, but we want to be fair (and make things simple) so we'll assume there are 460,000 asteroids interesting enough to want to visit, or one every 10
22
cm
2
within the Belt. That means the asteroids lie on an average of 10
11
cm apart, which happens to be 10
6
km or one million kilometers, about three times the distance from Earth to the Moon.
__________
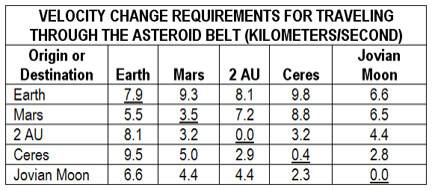
Values above the diagonal are delta-v requirements for travel from surface to surface, except when the starting point is Earth. All values for Earth assume beginning and end in Earth orbit.
Diagonal
values are circular orbit velocities. Values below the diagonal are those required for a trip that begins and ends in circular orbit. (Example: Ceres orbit to Mars orbit requires delta v of 5km/sec, while dirtside Ceres to dirtside Mars takes 8.8 km/sec.)
__________