A Field Guide to Lies: Critical Thinking in the Information Age (2 page)
Read A Field Guide to Lies: Critical Thinking in the Information Age Online
Authors: Daniel J. Levitin

PART ONE
EVALUATING NUMBERS
It ain’t what you don’t know that gets you into trouble.
It’s what you know for sure that just ain’t so.
—MARK TWAIN
P
LAUSIBILITY
Statistics, because they are numbers, appear to us to be cold, hard facts. It seems that they represent facts given to us by nature and it’s just a matter of finding them. But it’s important to remember that
people
gather statistics.
People choose what to count, how to go about counting, which of the resulting numbers they will share with us, and which words they will use to describe and interpret those numbers. Statistics are not facts. They are interpretations. And your interpretation may be just as good as, or better than, that of the person reporting them to you.
Sometimes, the numbers are simply wrong, and it’s often easiest to start out by conducting some quick plausibility checks. After that, even if the numbers pass plausibility, three kinds of errors can lead you to believe things that aren’t so: how the numbers were collected, how they were interpreted, and how they were presented graphically.
In your head or on the back of an envelope you can quickly determine whether a claim is plausible (most of the time). Don’t just accept a claim at face value; work through it a bit.
When conducting plausibility checks, we don’t care about the exact numbers. That might seem counterintuitive, but precision isn’t important here. We can use common sense to reckon a lot of these: If Bert tells you that a crystal wineglass fell off a table and hit a thick carpet without breaking, that seems plausible. If Ernie says it fell off the top of a forty-story building and hit the pavement without breaking, that’s not plausible. Your real-world knowledge, observations acquired over a lifetime, tells you so. Similarly, if someone says they are two hundred years old, or that they can consistently beat the roulette wheel in Vegas, or that they can run forty miles an hour, these are not plausible claims.
What would you do with this claim?
In the thirty-five years since marijuana laws stopped being enforced in California, the number of marijuana smokers has doubled every year.
Plausible? Where do we start? Let’s assume there was only one marijuana smoker in California thirty-five years ago, a very conservative estimate (there were half a million marijuana arrests nationwide in 1982). Doubling that number every year for thirty-five years would yield more than 17 billion—larger than the population of the entire world. (Try it yourself and you’ll see that doubling every year for twenty-one years gets you to over a million: 1; 2; 4; 8; 16; 32; 64; 128; 256; 512; 1024; 2048; 4096; 8192; 16,384; 32,768; 65,536; 131,072; 262,144; 524,288; 1,048,576.) This claim isn’t just implausible, then, it’s impossible. Unfortunately, many people have trouble thinking clearly about numbers because they’re intimidated by them. But as you see, nothing here requires more than elementary school arithmetic and some reasonable assumptions.
Here’s another. You’ve just taken on a position as a telemarketer,
where agents telephone unsuspecting (and no doubt irritated) prospects. Your boss, trying to motivate you, claims:
Our best salesperson made 1,000 sales a day.
Is this plausible? Try dialing a phone number yourself—the fastest you can probably do it is five seconds. Allow another five seconds for the phone to ring. Now let’s assume that every call ends in a sale—clearly this isn’t realistic, but let’s give every advantage to this claim to see if it works out. Figure a minimum of ten seconds to make a pitch and have it accepted, then forty seconds to get the buyer’s credit card number and address. That’s one call per minute (5 + 5 + 10 + 40 = 60 seconds), or 60 sales in an hour, or 480 sales in a very hectic eight-hour workday with no breaks. The 1,000 just isn’t plausible, allowing even the most optimistic estimates.
Some claims are more difficult to evaluate. Here’s a headline from
Time
magazine in 2013:
More people have cell phones than toilets.
What to do with this? We can consider the number of people in the developing world who lack plumbing and the observation that many people in prosperous countries have more than one cell phone. The claim seems
plausible
—that doesn’t mean we should accept it, just that we can’t reject it out of hand as being ridiculous; we’ll have to use other techniques to evaluate the claim, but it passes the plausibility test.
Sometimes you can’t easily evaluate a claim without doing a bit of research on your own. Yes, newspapers and websites really ought to be doing this for you, but they don’t always, and that’s how runaway statistics take hold. A widely reported statistic some years ago was this:
In the U.S., 150,000 girls and young women die of anorexia each year.
Okay—let’s check its plausibility. We have to do some digging. According to the U.S. Centers for Disease Control, the annual number of deaths
from all causes
for girls and women between the ages of fifteen and twenty-four is about 8,500.
Add in women from twenty-five to forty-four and you still only get 55,000. The
anorexia deaths in one year cannot be three times the number of
all
deaths.
In an article in
Science
, Louis Pollack and Hans Weiss reported that since the formation of the Communication Satellite Corp.,
The cost of a telephone call has decreased by 12,000 percent.
If a cost decreases by 100 percent, it drops to zero (no matter what the initial cost was). If a cost decreases by 200 percent, someone is paying
you
the same amount you used to pay
them
for you to take the product. A decrease of 100 percent is very rare;
one of 12,000 percent seems wildly unlikely. An article in the peer-reviewed
Journal of Management
Development
claimed a
200 percent reduction in customer complaints following a new customer care strategy.
Author Dan Keppel even titled his book
Get What You Pay For: Save 200% on Stocks, Mutual Funds, Every Financial Need.
He has an MBA. He should know better.
Of course, you have to apply percentages to the same baseline in order for them to be equivalent. A
50 percent reduction in salary cannot be restored by increasing your new, lower salary by 50 percent, because the baselines have shifted. If you were getting $1,000/week and took a 50 percent reduction in pay, to $500, a 50 percent increase in that pay only brings you to $750.

Percentages seem so simple and incorruptible, but they are often confusing. If interest rates rise from 3 percent to 4 percent, that is an increase of 1 percentage point, or 33 percent (because the 1 percent rise is taken against the baseline of 3, so 1/3 = .33). If interest rates fall from 4 percent to 3 percent, that is a decrease of 1 percentage point, but not a decrease of 33 percent—it’s a decrease of 25 percent (because the 1 percentage point drop is now taken against the baseline of 4). Researchers and journalists are not always scrupulous about
making this distinction between percentage point and percentages clear, but you should be.
The
New York Times
reported on the
closing of a Connecticut textile mill and its move to Virginia due to high employment costs. The
Times
reported that employment costs, “wages, worker’s compensation and unemployment insurance—are 20 times higher in Connecticut than in Virginia.” Is this plausible? If it were true, you’d think that there would be a mass migration of companies out of Connecticut and into Virginia—not just this one mill—and that you would have heard of it by now. In fact, this was not true and the
Times
had to issue a correction. How did this happen? The reporter simply misread a company report. One cost, unemployment insurance, was in fact twenty times higher in Connecticut than in Virginia, but when factored in with other costs, total employment costs were really only 1.3 times higher in Connecticut, not 20 times higher. The reporter did not have training in business administration and we shouldn’t expect her to. To catch these kinds of errors requires taking a step back and thinking for ourselves—which anyone can do (and she and her editors should have done).
New Jersey adopted
legislation that denied additional benefits to mothers who have children while already on welfare. Some legislators believed that women were having babies in New Jersey simply to increase the amount of their monthly welfare checks. Within two months, legislators were declaring the “family cap” law a great success because births had already fallen by 16 percent. According to the
New York Times:
After only two months, the state released numbers suggesting that births to welfare mothers had already fallen by 16 percent, and officials began congratulating themselves on their overnight success.
Note that they’re not counting pregnancies, but births. What’s wrong here? Because it takes nine months for a pregnancy to come to term, any effect in the first two months cannot be attributed to the law itself but is probably due to normal fluctuations in the birth rate (birth rates are known to be seasonal).
Even so, there were other problems with this report that can’t be caught with plausibility checks:
. . . over time, that 16 percent drop dwindled to about 10 percent as the state belatedly became aware of births that had not been reported earlier. It appeared that many mothers saw no reason to report the new births since their welfare benefits were not being increased.
This is an example of a problem in the way statistics were collected—we’re not actually surveying all the people that we think we are. Some errors in reasoning are sometimes harder to see coming than others, but we get better with practice. To start, let’s look at a basic, often misused tool.
The pie chart is an easy way to visualize percentages—how the different parts of a whole are allocated. You might want to know what percentage of a school district’s budget is spent on things like salaries, instructional materials, and maintenance. Or you might want to know what percentage of the money spent on instructional materials goes toward math, science, language arts, athletics, music,
and so on. The cardinal rule of a pie chart is that the percentages have to add up to 100. Think about an actual pie—if there are nine people who each want an equal-sized piece, you can’t cut it into eight. After you’ve reached the end of the pie, that’s all there is. Still, this didn’t stop Fox News from publishing this pie chart:
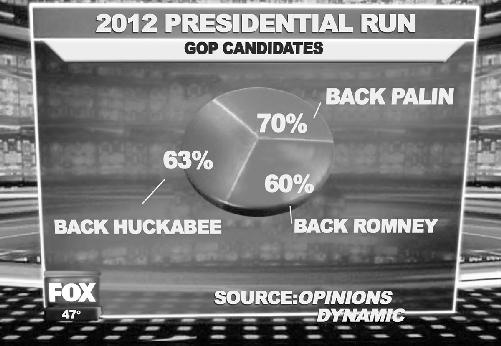
First rule of pie charts: The percentages have to add up to 100. (
Fox News, 2010
)
You can imagine how something like this could happen. Voters are given the option to report that they support more than one candidate. But then, the results shouldn’t be presented as a pie chart.
F
UN
WITH
A
VERAGES
An average can be a helpful summary statistic, even easier to digest than a pie chart, allowing us to characterize a very large amount of information with a single number. We might want to know the average wealth of the people in a room to know whether our fund-raisers or sales managers will benefit from meeting with them. Or we might want to know the average price of gas to estimate how much it will cost to drive from Vancouver to Banff. But averages can be deceptively complex.
There are three ways of calculating an average, and they often yield different numbers, so people with statistical acumen usually avoid the word
average
in favor of the more precise terms
mean, median,
and
mode.
We don’t say “mean average” or “median average” or simply just “average”—we say
mean,
median,
or
mode.
In some cases, these will be identical, but in many they are not. If you see the word
average
all by itself, it’s usually indicating the mean, but you can’t be certain.
