The Cosmic Landscape (8 page)

Feynman combined these basic ingredients, propagators and vertices, to make more complex processes. Here is an interesting one.
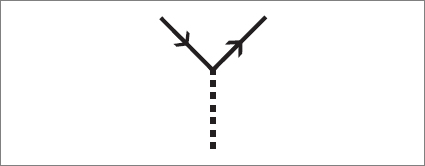
Can you see what it describes? If you use the cardboard-with-slit to view the diagram, here is what you will see: initially, at the lower part of the diagram, there are only an electron and a photon. Without warning, the photon spontaneously becomes an electron-positron pair. Then the positron moves toward the electron, where it meets its twin, and together they annihilate, leaving a photon. In the end there are a single photon and a single electron.
Feynman had another way to think about such diagrams. He pictured the incoming electron as “turning around in time” and temporarily moving toward the past, then turning around again toward the future. The two ways of thinking—either in terms of positrons and electrons or in terms of electrons moving backward in time—are completely equivalent. Propagators and vertices: that’s all there is to the world. But these basic elements can be combined in an infinite variety of ways to describe all of nature.
But aren’t we missing something important? Objects in nature exert forces on one another. The idea of force is deeply intuitive. It is one of the few concepts in physics that nature has equipped us to understand without consulting a textbook. A man pushing a boulder is exerting a force. The boulder is resisting by pushing back. The gravitational attraction of the earth keeps us from floating away. Magnets exert forces on pieces of iron. Static electricity exerts forces on bits of paper. Bullies shove wimps. The idea of force is so basic to our lives that evolution made sure that we had a concept of force built into our neural circuitry. But much less intuitive is the fact that all forces originate from attraction and repulsion between elementary particles.
Did Feynman have to add a separate set of ingredients to the recipe: specific rules of force between particles? He did not.
All forces in nature derive from special
exchange diagrams,
in which a particle like a photon is emitted by one particle and absorbed by another. For example, the electric force between electrons comes from a Feynman diagram in which one electron emits a photon, which is subsequently absorbed by the other electron.
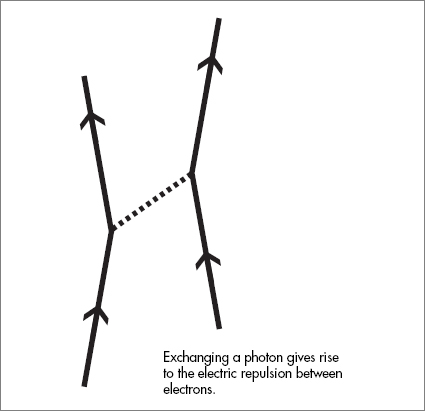
The photon jumping across the gap between the electrons is the origin of the electric and magnetic forces between them. If the electrons are at rest, the force is the usual electrostatic force that famously diminishes according to the square of the distance between the charges.
12
If the electrons happen to be moving, there is an additional magnetic force. The origin of both the electric and magnetic force is the same basic Feynman diagram.
Electrons are not the only particles that can emit photons. Any electrically charged particle can, including a proton. This means that photons can hop between two protons or even between a proton and an electron. This fact is of enormous importance to all of science and life in general. The continual exchange of photons between the nucleus and the atomic electrons provides the force that holds the atom together. Without those jumping photons, the atom would fly apart, and all matter would cease to exist.
Tremendously complicated Feynman diagrams—networks of vertices and propagators—represent complex processes involving any number of particles. In this way Feynman’s theory describes all matter from the simplest to the most complicated objects.
Feel free to add arrows to this picture in various ways to make the solid lines into electrons or positrons.
The various equations and formulas of physics contain a variety of different numerical constants. Some of these constants are numbers derived from pure mathematics. An example is the number 3.14159… , better known by its Greek name, π. We know the value of π to billions of decimal places, not by measuring it, but from its purely mathematical definition: π is defined to be the ratio of the circumference of a circle to its diameter. Other purely mathematical numbers, such as the square root of 2 and the number called
e
, may also be computed to endless precision if anyone were motivated to do it.
But other numbers that appear in physics equations have no special mathematical significance. We might call them empirical numbers. An example that is important in nuclear physics is the ratio of the proton mass to the neutron mass. Its numerical value is known to seven figures—1.001378. The next digit cannot be obtained by mathematics alone. One must go into the lab and measure it. The most fundamental of these empirical numbers are crowned with the title “constants of nature.” The fine structure constant is one of the most important constants of nature.
13
Like π, the fine structure is named for a Greek letter, in this case α (alpha). It is often approximated by the fraction
1
/
137
. Its precise value is known to a limited number of decimal places—0.007297351—but it is, nonetheless, one of the most accurately known physical constants.
The fine structure constant is an example of a quantity that physicists call
coupling constants.
Each coupling constant is associated with one of the basic events—the vertex diagrams—of quantum field theory. The coupling constant is a measure of the
strength,
or
potency,
of the event depicted by the vertex. In QED the sole vertex diagram is the emission of a photon by an electron. Let’s consider more closely what happens when a photon is emitted.
One might begin by asking what determines the precise point at which an electron, as it moves through space-time, emits a photon. The answer is that nothing does—physics at the microscopic level is capricious. Nature has a random element that drove Einstein in his later years to distraction. He protested, “God does not play dice.”
14
But whether Einstein liked it or not, nature is not deterministic. Nature has an element of randomness that is built into the Laws of Physics at the deepest level. Even Einstein couldn’t change that. But if nature is not deterministic, neither is it completely chaotic. Here is where the principles of quantum mechanics enter. Unlike Newtonian physics, quantum mechanics never predicts the future in terms of the past. Instead, it provides very precise rules for computing the probability for various alternative outcomes of an experiment. Just as there is no way to predict the final location of a photon that has gone through a slit, there is also no way to predict exactly where along its path an electron will launch a photon or where another electron may absorb it. But there is a definite probability for these events.
The operation of a television screen provides a good illustration of such probabilities. The light coming from a TV screen is composed of photons that are created when electrons strike the screen. The electrons are ejected from an electrode at the rear of the set and are guided to the screen by electric and magnetic fields. But not every electron that hits the screen emits a photon. Some do. Most don’t. Roughly speaking the probability that any particular electron will radiate a quantum of light is given by the fine structure constant α. In other words, only one lucky electron out of 137 emits a photon. That is the meaning of α: it is the probability that an electron, as it moves along its trajectory, will capriciously emit a photon.
Feynman didn’t just draw pictures. He invented a set of rules for working out the probabilities of the complex processes depicted in the pictures. In other words, he discovered a precise mathematical calculus that predicts the probabilities for any process in terms of the simplest events—propagators and vertices. The probabilities for all processes in nature ultimately trace back to coupling constants like a.
The fine structure constant also controls the strength of the exchange diagrams, which in turn, determine the strength of electric forces among charged particles. It controls how tightly the atomic nucleus pulls the electrons toward it. As a consequence it determines how big the atom is, how fast the electrons move in their orbits, and ultimately controls the forces between different atoms that allow them to form molecules. But as important as it is, we don’t know why its value is 0.007297351 and not something else. The Laws of Physics that were discovered during the twentieth century are very accurate and useful, but the underlying origin of those laws remains a mystery.
The theory of this simplified world of electrons, photons, and point nuclei is Quantum Electrodynamics, and Feynman’s version of it was incredibly successful. Using his methods the properties of electrons, positrons, and photons were understood with astonishing accuracy. Moreover, if the simplified version of the nucleus was added, the properties of the simplest atom—hydrogen—could also be calculated to incredible precision. In 1965 Feynman, Julian Schwinger, and the Japanese physicist Sin-Itero Tomanaga won the Nobel Prize for their work on Quantum Electrodynamics. That was Act I.
If Act I was theater in the small, with only two characters, the play became an epic with hundreds of players in Act II. New particles were discovered throughout the 1950s and 1960s that eventually required an unruly cast including electrons, neutrinos, muons, tau particles, up-quarks, down-quarks, strange-quarks, charmed-quarks, bottom-quarks, top-quarks, photons, gluons, W- and Z-bosons, Higgs bosons, and a good deal more. Don’t ever believe anyone who tells you that elementary-particle physics is elegant. This hodgepodge of particle names reflects an equally unwieldy jumble of masses, electric charges, spins, and other properties. But as messy as it is, we know how to describe it with enormous precision. The Standard Model is the name of the mathematical structure—a particular quantum field theory—that describes the modern theory of elementary particles. Although it is far more complicated than Quantum Electrodynamics, Feynman’s methods are so powerful that, once again, they can be used to express everything in terms of simple pictures. The principles are exactly the same as those of QED: everything is built out of propagators, vertex diagrams, and coupling constants. But there are new actors and whole new plot lines, including one called QCD.
