The Cosmic Landscape (45 page)

Singularities in higher dimensional spaces—places where the space is not smooth—are more complicated. They have more complex topology. The conifold is one such singularity that can exist on a Calabi Yau space. Although complicated, as its name suggests, it is similar to the tip of a cone. For our purposes we can think of the conifold as a pointy conical place in the geometry.
An interesting thing happens when you combine conifolds and fluxes on the same Calabi Yau space. The flux exerts a force on the tip of the cone, stretching it out into a long, narrow neck like the snout of an anteater. In fact you can have more than one conifold singularity so that the space becomes spiky with pointy tips sticking out like some six-dimensional sea urchin.
Now Rube has the parts. What kind of screwball machine can he build? The possibilities are enormous, but I’ll describe one machine called the KKLT construction, named for the first initials in the last names of its founders.
2
KKL and T began with a Calabi Yau space. There are millions to choose from. Just take your pick. Somewhere on the space there is a snouty conifold singularity. Next KKLT filled the various holes with fluxes: an integer for each hole. All of this meant specifying about five hundred parameters—moduli and fluxes. The result is a valley on the Landscape, but not like any we have talked about yet. This point is the Death Valley of the Landscape—not because it is hot—but because it is below sea level. The altitude is negative. This of course means that the vacuum energy, and therefore, the cosmological constant, is negative—the wrong sign for our universe. Instead of giving rise to a universal repulsion, it would cause a universal cosmic attraction. Instead of accelerating the expansion of the universe, it would hasten the tendency to collapse.
But KKLT had one more Rube Goldberg trick. They added an antibrane—an anti-carpet-brane. D-branes are like particles. Just as every particle has its antiparticle, every brane has its antibrane. Like ordinary particles, if a brane and an antibrane come together, they can annihilate in an explosion of energy. But KKLT put only antibranes into their construction.
As it turns out the antibrane experiences a force that pulls it toward the tip of the conifold singularity. That is the only possible location for the antibrane. The mass of the extra antibrane adds just enough energy to make the altitude positive. Thus, by a mix of a little bit of everything, KKLT discovered a point on the landscape, a valley really, with a small positive cosmological constant—the first of its kind.
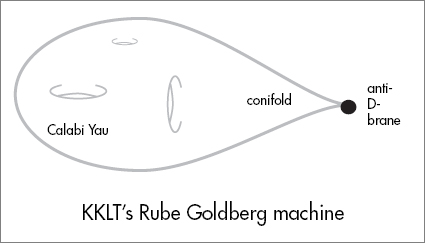
The importance of the valley that KKLT discovered is not that it closely resembles our own valley. It has no Standard Model of particle physics, and in the original form, it didn’t have the ingredients to describe Inflation. Its significance is that it is the first successful attempt to depart from the supersymmetric plain and find a valley “above sea level.” It was proof of a principle—that the String Theory Landscape has valleys with a small positive cosmological constant.
The KKLT machine does have a feel of Rube Goldberg complexity, but it has one feature that Rube never would have permitted. It has one part that serves two purposes. The antibrane not only raises the energy and makes the cosmological constant positive, but it also does another important job. Our world, the world that we live in, is not supersymmetric. There is no massless fermion partner of the photon, no bosonic identical twin for the electron. Before putting the antibrane down the conifold throat, the KKLT construction was still supersymmetric. But the antibrane warps the funhouse mirror so that supersymmetry is broken. That’s very un-Goldberg-like—to use one part to do two jobs.
The KKLT point on the Landscape is not our world. But it may not be so hard to build in the Standard Model by including a few more branes. Somewhere out of the way of the antibrane, five additional D-branes could provide the extra ingredients.
What KKLT found was not a single valley but rather a vast collection of valleys. As I mentioned at the start of chapter 7, Polchinski and Raphael Bousso, then a postdoc at Stanford, had already explained the basic idea in a largely ignored paper. To understand how compactification can lead to tremendous numbers of vacuums, Bousso and Polchinski had concentrated on a single Calabi Yau geometry and asked how many ways there are to fill hundreds of donut holes in the space with fluxes.
Let’s suppose that the Calabi Yau manifold has a topology that is rich enough to allow five hundred distinct donut holes through which the fluxes wind. The flux through each hole must be an integer, so a string of five hundred integers has to be specified.
Theoretically there are no limits on the size of the integers, but in practice we would not want to put too much flux through any hole. The effect of a very large flux would be to stretch out the size of the manifold to proportions that might be dangerous. So let’s make some limits. Suppose that the flux integers are constrained to be no bigger than nine. Then each of the fluxes is an integer between zero and nine. How many possibilities does that add up to?

Let’s begin with an easier example. Suppose there is only one hole to deal with instead of five hundred. If the flux through the hole can be any integer between zero and nine, then there are ten possibilities—zero, one, two, three, four, five, six, seven, eight, and nine. The point is that each of these possibilities defines a potential vacuum, an environment with its own laws and, most important, its own vacuum energy. Although ten vacuums are a lot from the perspective of ordinary twentieth-century quantum field theory, it is hardly a promising number for overcoming the incredible improbability of 119 vanishing decimal entries. But let’s continue.
Suppose there are two holes, each of which can have flux between zero and nine. Then the number of possible configurations is 10
2
, or one hundred. This is slightly better but still far too modest. But note that each time a hole is added, the number of possibilities grows ten times larger. Six holes give a million possibilities; twelve holes give one trillion. With five hundred holes we get the stupendously large number of configurations 10
500
. Moreover, each valley in this gargantuan list has some vacuum energy, and no two of them are likely to have exactly the same value.
Let’s make a chart to show all the possible values of the cosmological constant. Take a sheet of paper and draw a horizontal axis. Halfway along the line mark a point and call it zero. At the right mark a point and call it one. The value one stands for the benchmark value of the vacuum energy—one Unit. Now start marking all the points that correspond to the vacuum energies of the 10
500
valleys. With a very sharp pencil you may be able to make one thousand random dots before they begin to run into one another and make a continuous line.
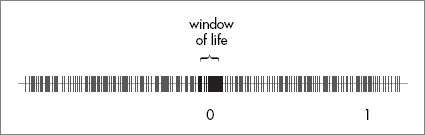
To do better get a bigger sheet. With a sheet as big as the Empire State Building, you may get a million randomly placed dots before they start to touch. With a page the size of the galaxy, perhaps 10
24
points can be shown. None of these numbers is anywhere near 10
500
. Even if you spaced the points a Planck length apart and made the sheet as big as the known universe, you would get only a measly 10
60
points. The number 10
500
is so staggeringly large that I can’t think of any way of graphically representing that many points.
The word for
all
possible numbers in a given range is
continuum.
The points on our vacuum energy plot do not really form a continuum, but they are so dense that for practical purposes every number is represented. To describe such a terrifically large and dense set of values, string theorists like Bousso and Polchinski coined the word
discretuum
—discrete but almost a continuum.
But the real point is that with that many randomly chosen values for the cosmological constant, there will be a huge number in the tiny “window of life” that Weinberg calculated. No fine-tuning is needed to make sure of that. Of course it will be only a minute fraction of the valleys that are in the anthropic window of opportunity—roughly one out of 10
120
.
The growth of the Landscape over the years since String Theory was discovered has been a source of anguish for most string theorists. During the happy early days, when the impoverished Landscape was composed of only a single point or, at most, a number that could be counted on the fingers of one hand, string theorists were overjoyed when they found that the few known theories were really just different solutions of a single theory. But as this consolidation was taking place, another more ominous trend was developing that horrified many string theorists. The number of distinct solutions was expanding into an unimaginably large Landscape. But I suspect that, in time, these same string theorists will begin to see the Landscape as the single most important and convincing feature of their theory. One might ask, “Haven’t we just substituted one impossible problem for another? No longer do we have to wonder why the cosmological constant is so fine-tuned. Perhaps it’s true that the Landscape is so prodigious that you can find whatever you are looking for. But what principle of physics picks out our benign valley from 10
500
others?” The answer that we will come to in the next chapter is that nothing does. As we will see, the question is the wrong one.
A Bubble Bath Universe
I
t’s one thing to argue that theory gives rise to many possibilities for the Laws of Physics, but it’s quite another to say that nature actually takes advantage of all the possibilities. Which of the many possible environments materialized as real worlds? The equations of physics undoubtedly have solutions describing giant spherical shells of stainless steel orbiting around massive “stars” made of pure gold. In a theoretician’s sense such solutions of the equations
exist.
But are there any such objects in the universe? Probably not, and the reasons are historical. Nothing about the way the universe evolved—nothing about Big Bang cosmology—could explain how such objects could ever have formed. Mathematical existence is not the same as physical existence obviously. Discovering that String Theory has 10
500
solutions explains nothing about our world unless we also understand how the corresponding environments came into being.
Some physicists believe that there must be a
vacuum selection principle
that singles out a unique point in the Landscape—presumably our point. Such a principle, if it exists, might be mathematical—perhaps a proof that only one of the many apparent solutions of String Theory is really consistent. But, if anything, the mathematics of String Theory has gone the other way—toward greater and greater nonuniqueness. I have heard some say that the vacuum selection principle must be cosmological; the birth of the universe could happen only in a unique way leading to an equally unique environment. But the vacuum selection principle is a lot like the Loch Ness monster: it’s often claimed to exist, but no one has ever seen it. Consequently, many of us are beginning to suspect that it doesn’t exist at all. Even if such a mechanism does exist, the chances that the resulting Laws of Physics would be fine-tuned to the incredible precision needed for our existence would still be negligible. My own feeling is that a true vacuum selection principle would most likely be a disaster.
