The Cosmic Landscape (33 page)

The resulting single string is usually left in an excited state vibrating and rotating. But after a short time, like the chain of dancers, the string can break in two by reversing the process that joined the original strings. The net result is an operation in which a pair of strings comes together, forms a compound string, and then splits back into two strings.

The problem that I had solved in the attic was this: suppose two mesons (strings) were originally moving with a given energy in opposite directions before they collided. What is the quantum-mechanical probability that, after they collide, the resulting pair of strings will be moving along some specified new direction? It sounds like a horribly complicated problem, and it was something of a mathematical miracle that it could be solved.

The mathematical problem of describing an idealized elastic string had already been solved by the early nineteenth century. A vibrating string can be viewed as a collection of harmonic oscillators, one for each separate type of oscillating motion. The harmonic oscillator is one of the few physical systems that can be completely analyzed with very simple high school mathematics.

Adding quantum mechanics to make the string a quantum object was also simple. All that was necessary was to remember that the energy levels of any oscillating system come in discrete units of energy (see chapter 1). This simple observation was sufficient to understand the properties of a single vibrating string; but describing two interacting strings was much more intricate. For that I had to work out my own rules from scratch. What made it possible was that the complexity lasts for only an infinitesimal instant of time when the ends touch and join. Once that happens the two strings become one string, and the simple math of a single string takes over. A little later the single string splits, but again, the complicated event takes only an instant. Thus, with great precision, I was able to follow the two strings as they merged and separated. The results of the mathematical calculation could be compared with Veneziano’s formula, and gratifyingly, they agreed exactly.

Baryons are three strings joined at the center, and mesons are a single string with two ends, but what are glueballs? Start with a single chain of dancers. As the dancers move in complicated steps, every so often the two end dancers may run into each other. Not realizing that they belong to the same chain, they clasp hands. The result is a closed circle of dancers with no free end. The same thing can happen to a vibrating meson. In the course of moving, vibrating, and rotating, the two ends come close together. The quark at one end sees the antiquark at the other and doesn’t care that it happens to be attached to the same string. It grabs the end like a snake mistaking its tail for a tasty meal. The result is a glueball: a closed loop of string with no ends and no quarks. Many mesons and baryons were known to exist long before String Theory came along, but glueballs were a prediction of String Theory. Today, if you look at a list of the known particles, glueballs and their masses will be listed along with baryons and mesons.

Mesons, baryons, and glueballs are complex objects that can vibrate and oscillate in all sorts of patterns. For example, the string connecting the ends of a meson can vibrate like a spring or even a violin string: it can even spin around an axis, with centrifugal force stretching it out to form a whirling, propeller-like hadron. These “excited states” of hadrons are also well-known objects, some of which were discovered in experiments as early as the 1960s.

The connection between the String Theory of hadrons and the Laws of Physics, particularly their expression in terms of Feynman diagrams, is far from obvious. One way of looking at it is that String Theory is a generalization of Feynman diagrams in which a string replaces each point particle. Feynman diagrams are composed from basic units that we discussed in chapter 1: propagators and vertices. Propagators and vertices make a great deal of sense for the infinitely small
point particles
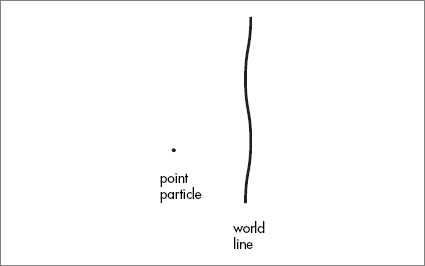
of quantum field. For example, the vertex itself is the point at which the particle trajectories meet. If the particles themselves are not points, it is not at all clear what is meant by the point at which they meet. Here’s how the ideas of propagator and vertex make sense for strings. If we start with a point particle and imagine it moving through space-time, it traces out a curve. At each instant it is a point, but as time unfolds, the points trace out a curve. The great Minkowski called such a path through space-time a
world line,
and the terminology stuck.

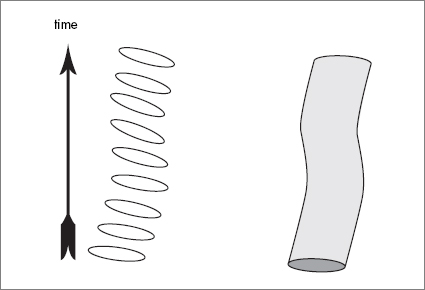
Now let’s try to envision the history of a string. Let’s take the case of a closed string with no ends. At any instant of time, the string is just a closed curve (loop) through space. Imagine a stroboscope illuminating the string. The first instant we see a loop. The next instant we see the same loop, but now it may have moved to a slightly different location in space. This pattern repeats so that as time unfolds we see a series of loops in space-time, one stacked above the next.

But time really evolves continuously, not in sudden flashes like a stroboscopically lit disco. To represent the history of the string, we need to fill in the spaces between the flashes. The result is a tube through space: a two-dimensional cylinder.

The size of the loop of string might change from one instant to the next. Strings are, after all, like elastic, stretchable rubber bands. They can even get twisted into figure eights or more complex shapes. In that case the neat cylinder will be deformed but still recognizable.

The surfaces swept out in this way could well be called world tubes, in analogy with the world line of the point particle. As it happened that was not the term I originally used to describe them. Instead I used the term
world sheet,
and again, the terminology stuck. But whichever they are called, the cylinder-like world sheet of a string replaces the propagator of the point particle.

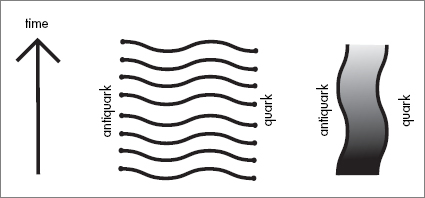
A meson with its quark ends may also be described by a world sheet: not a cylinder, but a ribbon with two edges. Again start with the stroboscopic history. This time we see a sequence of open strings, each with a quark and an antiquark at its ends. Filling in the spaces gives the ribbonlike world sheet.

But an interesting theory that can describe all the complexity of interacting colliding particles needs more than just propagators. It also needs vertex diagrams, forks in the road that allow particles to emit and absorb other particles. String Theory is no different.

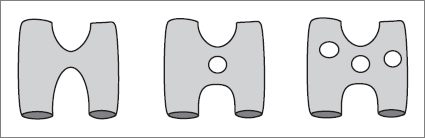
For an open string the vertex is replaced by the splitting process in which a single string splits in two with a new quark-antiquark pair created at the newly formed ends. Closed strings can also divide by a kind of plumbing diagram, where a single pipe divides; call it a Y-joint.

If you follow the action from bottom to top (past to future), you will see a single, closed string splitting and becoming two separate strings that each go off in its own direction. You can also turn the diagram over and see two strings coming together and fusing, to form a single string.

The idea is that plumbing networks, built up from string propagators and Y-joints, replace the usual Feynman diagrams. It was understood very early that the division of a diagram into cylindrical propagators and Y-joints was an artificial one and that the theory was really about world sheets of any shape and topology. The diagrams have openings representing the incoming and outgoing stringlike glueballs, but otherwise they can be of any complexity.

This way of thinking about hadrons is hard to connect with the Standard Model, a theory based on conventional Feynman diagrams (i.e., point particles). The modern Standard Model has what at first sight seems to be an entirely different theory of hadrons—the theory known as Quantum Chromodynamics, or QCD.

According to QCD, hadrons are made of quarks and antiquarks. That much QCD has in common with the String Theory that Nambu and I discovered. But the binding force—the glue—that holds the quarks together has nothing obvious to do with strings. In the same way that an electron can emit a photon, quarks can emit (and absorb) gluons. These gluons, being exchanged between quarks, explain the forces that bind the quarks into hadrons.

Gluons have one feature that makes them more complicated than photons. Charged particles can emit and absorb photons, but photons themselves do not have the capacity to emit photons. Another way to say the same thing is that there is no vertex in which a single photon splits into two photons. Gluons themselves do have this capacity. There is a vertex diagram in which three gluons come together at the vertex. Ultimately this makes gluons and quarks a lot stickier than electrons and positrons.