The Cosmic Landscape (26 page)

Vacuum energy or mass has an unusual property. Ordinary mass density, like that due to the galaxies, dilutes when the universe grows. The mass density in the form of ordinary matter is about one proton per cubic meter. Suppose the radius of the universe doubled over some billions of years but the number of protons in the universe remained fixed. Then the mass density would obviously decrease. In fact it would decrease by a factor of eight. Double the radius again, and the number of protons per cubic meter decreases to one sixty-fourth of its present value. The same is true of the dark-matter component.

But vacuum energy is very different. It’s a property of empty space. When empty space expands it’s still just empty space, and the energy density is exactly what it was originally. No matter how many times you double the size of the universe, the vacuum energy density stays the same, and its repulsive effect never diminishes!

By contrast, ordinary matter thins out and eventually becomes ineffective at slowing down the expansion. After a sufficient amount of expansion, all forms of energy will be diluted away except for vacuum energy. Once this happens there is nothing to counteract the repulsive effects of the vacuum energy, and the universe expands exponentially. If the cosmological constant were large enough to double the size of the universe in one second (it’s not), then it would become four times as big in two seconds, eight times as big in three seconds, sixteen times, thirty-two times, and so on. Things that are close to us now would soon be rocketing away faster than the speed of light.

The real universe is in the early stages of this kind of exponential expansion. It won’t bother us very much since the cosmological constant is only strong enough to double the size of the universe over a period of tens of billions of years. But imagine that for some unknown reason, in the very early universe, the cosmological constant were much bigger, perhaps a hundred orders of magnitude bigger. This may sound like a strange thought experiment, but remember that the hard thing to understand is why today’s cosmological constant is so ridiculously small. Make it one hundred orders of magnitude larger, and it becomes ordinary, at least from the theoretical physicists’ point of view.

If the cosmological constant were that big early on, it would cause the universe to double in a tiny fraction of a second. In one second the universe would grow from the size of a proton to something vastly larger than the known universe. This is real Inflation of the kind envisioned by Starobinsky and Guth.

The reader may wonder what kind of double-talk allows me to speak of different cosmological constants in the early and late universe, i.e., during Inflation and now. After all, aren’t constants constant? Stop now and think
Landscape.
The cosmological constant in a given region of the Landscape is nothing but the local altitude. A picture of a bit of Landscape is worth a thousand words.
⁹
The picture below is a very simplified version of a Landscape that might resemble our neighborhood. The little ball represents the universe, rolling along, seeking a valley where the vacuum energy is minimum.

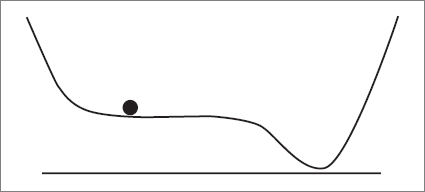
Some unknown history of the universe placed it on a relatively broad, high shelf overlooking a deep valley of almost zero altitude (here is where Guth’s Inflation begins). How the universe arrived on the shelf is a question for another day. Because the shelf is so flat, the universe rolled very slowly at first. While it was on the shelf, the vacuum energy (altitude) was practically unchanging. To state it differently, the altitude of the plateau served as a cosmological constant while the universe was resting on the shelf.

And, as I’m sure you guessed, as it slowly rolled, it inflated because the vacuum energy was large and positive. If the shelf was flat enough and the rolling slow enough, the universe would double many times before coming to the steep descent down to the valley. This was the inflationary era, although in a more modern form than Starobinsky and Guth first proposed. If the universe doubled one hundred times or more during this period, it would have grown to such large proportions that it would be as flat and homogeneous as the CMB requires.

Eventually the rolling brought the universe to the edge of the shelf and then down into the valley, where it came to rest. If the altitude at that point is not quite zero, then the long-term future of the universe will have a small cosmological constant. If by chance the cosmological constant is small enough in the valley, and other conditions are right, galaxies, stars, planets, and life could form. If not, that particular pocket would be sterile. All of known cosmology took place during a roll from one value of the cosmological constant to a much smaller one. Can anyone seriously doubt that there was more to the history and geography of the universe than this brief episode and this tiny pocket?

But wait! Something is wrong with this picture. If the universe inflates to such a large degree, it can be expected to be incredibly homogeneous. All the wrinkles would have been ironed out so completely that there would be no variations at all in the CMB. But we know that without some small wrinkles to seed the galaxies, the universe would have remained smooth indefinitely. We seem to have overdone the homogenizing.

The solution to this puzzle involves an idea so radical and surprising that at first you might be tempted to dismiss it as pie-in-the-sky speculation. But it has withstood the test of time and is currently one of the cornerstones of modern cosmology. Once again its initial discovery took place in Russia, by a young cosmologist named Slava Mukhanov, who was studying Starobinsky’s work. History repeats itself: Mukhanov’s work was unknown outside the USSR until several groups working in the United States independently rediscovered it.

Quantum mechanics and its jittery consequences are normally thought to apply to the world of the very small, not galaxies and other cosmic-scale phenomena. But it now appears all but certain that galaxies and other large-scale structures are remnants of original minute quantum fluctuations that were expanded and enhanced by the unrelenting effect of gravity.

The idea that the universe is at an exact point in the Landscape is a little too simple. Like everything else, quantum fields such as the Higgs field have the jitters. Quantum mechanics is enough to ensure that the fields do fluctuate from point to point in space. No amount of Inflation can iron out the random quantum fluctuations that every field must have. This is true in our vacuum today, and it was true during the rapid exponential expansion of Inflation. But rapid Inflation does something to these fluctuations that doesn’t happen to any appreciable degree in our very slowly expanding universe. It stretches out the old wrinkles but keeps replacing them with new ones. New wrinkles on top of old wrinkles, all expanding as the universe expands. By the time Inflation ended and the universe tipped over the edge of the ledge, the accumulated quantum wrinkles had built up and formed the minute density contrasts that eventually grew to become galaxies.

These frozen-in quantum wrinkles also imprinted themselves on the surface of last scattering, and we can see them as the tiny variations of brightness in the cosmic microwave vacuum. The connection between the quantum theory of the microscopic world and the large-scale structure of the astronomical and cosmological world is one of the greatest achievements of cosmology.

Let me finish this chapter by summarizing the two most important things we have learned from cosmological observations during the last decade. First, we have found a real shocker: there really is a cosmological constant. The first 119 decimal places cancel, but astonishingly, in the 120th the result is not zero!

The second point of enormous interest is that the theory of Inflation has strong support from the study of cosmic background radiation. The universe apparently grew exponentially for some period of time. It is all but certain that the entire universe is many, many orders of magnitude bigger than the part we can see.

These are both great discoveries, but they are also disturbing. If we reached into a bag of random numbers and pulled out generic values for the constants of nature, neither a small cosmological constant nor a suitable period of Inflation would be likely outcomes. Both require an enormous degree of fine-tuning. As we’ve seen before, the universe appears to have been specially designed. More about this specialness in the next chapter.

F
or explaining physics to an audience of nonphysicists, analogies and metaphors are obviously invaluable. But for me they are also tools for thought, my own idiosyncratic tools. Often I convince myself of the truth of some difficult point by inventing an analogy that applies similar questions to a more ordinary context.

The Anthropic Principle has created more confusion and irrelevant philosophical claptrap than anything that has come out of science for quite some time. Incessant argument occurs over its meaning, how it should be used to explain and predict, when it is legal, when it is not, when it is sensible, and when it is nonsense. The surest guide for me is to build an analogy about the more familiar world, where good old common sense can clear the air. More than a decade ago, I made up a parable to convince myself that the Anthropic Principle can make some sense.

It’s an old tradition for well-known physicists to celebrate their sixtieth birthdays with parties, but these birthday parties usually consist of a couple of long days of continuous physics seminars—without music. I had to give a lecture at one such party for an old friend, Martinus Veltman. Tini—a bristly, bearded, colorful ogre of a Dutchman—looked like a cross between Orson Welles playing Macbeth and Saddam Hussein when he came out of his spider hole. Tini recently won the Nobel Prize for his work with Gerard ’t Hooft that developed the mathematics of the Standard Model.

Because Tini was one of the first people to recognize the problem of vacuum energy, I thought I would give a birthday talk called “Tini and the Cosmological Constant.” What I wanted to speak about was the Anthropic Principle and Steve Weinberg’s calculation of galaxy formation. But I also wanted to explain how the Anthropic Principle could make good scientific sense. So as usual I made up an analogy.

Instead of asking why the cosmological constant is so precisely fine-tuned, I substituted a similar question: why is the temperature of the earth finely tuned to be in the narrow range in which liquid water can exist? Both questions ask how it happens that we live in a very unlikely environment that seems perfectly tailored to our own existence. To answer my question I proposed the following parable about intelligent fish.
¹

A Fish Story

Once upon a time, on a planet completely covered by water, lived a race of big-brained fish. These fish could survive only at a certain depth, and none had ever seen either the surface above or the bottom below. But their big brains made them very smart and also very curious. In time their questions about the nature of water and other things became very sophisticated. The most brilliant among them were called fyshicists. The fyshicists were wonderfully clever, and in a few generations they came to understand a great deal about natural phenomena, including fluid dynamics, chemistry, atomic physics, and even the nuclei of atoms.

Eventually some of the fyshicists began to question why the laws of nature are what they are. Their sophisticated technology allowed them to study water in all its forms, especially ice, steam, and of course, the liquid state. But with all their efforts still one thing stumped them. With all the possible values from zero to infinity, how could they account for the fact that the background temperature, T, was fine-tuned to be in the very narrow range that allowed H
₂
O to exist in its liquid form? They tried many things, including symmetries of various kinds, dynamical relaxation mechanisms, and many other ideas, but nothing could explain it.

Closely allied with the fyshicists were another group, the codmologists, who were also studying their watery world. The codmologists were less interested in the ordinary depths, where the big-brained fish lived, than they were in discovering if an upper boundary to their water-world existed. The codmologists were well aware that much of the water-world was not habitable, the pressure being wrong for their big brains. Journeying by fin to the upper reaches was by no means possible. Their big brains would explode if exposed to the very low water pressure in these regions. So instead, they speculated.

It happened that one school of thought among the codmologists held a very radical (some said ridiculous) idea about the fine-tuning of T. And they had a name for the idea—the Ickthropic Principle. The I.P. maintained that the temperature was in the liquid water range because only in this case could fish exist to observe it!

“Garbage!” said the fyshicists. “That’s not science. It’s religion. It’s just giving up. And besides, if we agree with you, everyone will laugh at us and take away our funding.”