Napoleon's Pyramids (21 page)
Read Napoleon's Pyramids Online
Authors: William Dietrich
Tags: #Historical, #Action & Adventure, #Egypt, #Gage; Ethan (Fictitious character), #Egypt - History - French occupation; 1798-1801, #Fiction, #Great Pyramid (Egypt), #Historical fiction; American, #Historical Fiction

“I thought this was the tomb of the pharaoh,” Talma said.
“A tomb with no occupant. When Arab treasure hunters broke in centuries ago and tunneled around granite plugs meant to seal the entrance forever, they found not a sign that any king, queen, or commoner had ever been laid to rest here. The sarcophagus was lidless and empty. There was no writing, and not a scrap of treasure or worldly goods to commemorate who it was built for. The greatest structure on the face of the earth, taller than the highest cathedrals, and empty as a peasant’s cupboard! It is one thing to be a megalomaniac, harnessing tens of thousands of men to build your final resting place. It is quite another to do so and not rest there.”
I looked as Ashraf, who had not followed our French. “What’s the pyramid for?” I asked in English.
He shrugged, less in awe of the monument than we were. Of course, he’d lived in Cairo all his life. “To hold up the sky.”
I sighed and turned back to Jomard. “So you think it’s a map?”
“That is one hypothesis. Another is that its dimensions signify the divine. For thousands of years, architects and engineers have recognized that some proportions and shapes are more pleasing than others. They correspond to each other in interesting mathematical ways. Some feel such sublime relationships reveal fundamental and universal truths. When our own ancestors built the great Gothic cathedrals, they tried to use their dimensions and geometric proportions to express religious ideas and ideals, to in effect make the building itself holy by its very design. ‘What is God?’ Saint Bernard once asked. ‘He is length, width, height, and depth.’”
I remembered Astiza’s excitement over Pythagoras.
“So?” Talma challenged.
“So this pyramid may have been, to the ancients who built it, not a picture of the world, but a picture of God.”
I stared uneasily at the vast structure, the hair prickling on my neck. It was utterly silent, and yet from nowhere I sensed a low, background hum, like the sound of a seashell pressed to the ear. Was God a number, a dimension? There was something godlike in the perfect simplicity before me.
“Unfortunately,” Jomard went on, “all these ideas are difficult to verify until measurements are made to confirm whether height and perimeter match in scale the dimensions of our earth. That will be impossible to do until we excavate enough to find the pyramid’s true base and corners. I’ll need a small army of Arab workmen.”
“I suppose we can go back then,” Talma said hopefully.
“No,” said Jomard. “We can at least begin to measure its height from the lowest course of stone we can see. Gage, you will help with the tape. Talma, you must take the utmost care to write down each stone height we give you.”
My friend looked dubiously upward. “All that way?”
“The sun is declining. By the time we reach the top, it will be cooler.”
Ashraf chose to remain below, clearly believing such a climb was something only sun-addled Europeans would do. And indeed, it wasn’t easy. The pyramid seemed far steeper once we began to mount it.
“An optical illusion makes it appear squatter than it is, when viewed head on,” Jomard explained.
“You didn’t tell us that before we started up,” Talma grumbled.
It took the three of us more than half an hour of careful ascent to get halfway. It was like climbing titanic children’s blocks, a giant’s staircase, with each step averaging two and a half feet in height. There was a real possibility of a nasty fall. We carefully measured each course of interior stone as we climbed, Talma keeping a running tally.
“Look at the size of these monsters,” the journalist said. “They must weigh several tons. Why not build with smaller pieces?”
“Some engineering reason, perhaps?” I suggested.
“There’s no architectural requirement for stones this big,” Jomard said. “Yet the Egyptians cut these behemoths, floated them on the Nile, dragged them up that hill, and somehow hoisted them this high. Gage, you’re our expert on electricity. Could they have used such a mysterious force to move these rocks?”
“If so, they had mastery of something we barely understand. I can devise a machine to give you a tingle, Jomard, but not to do any useful work.” Once again I felt inadequate to the mission I’d given myself. I looked around for something tangible to contribute. “Here’s something. Some of these stones have shells in them.” I pointed.
The French savant followed my finger. “Indeed!” he said with surprise. He bent to inspect the limestone I’d pointed to. “Not shells, but the fossils of shells, as if these blocks originated from beneath the sea. It’s a curiosity that has been noticed in mountain ranges in Europe, and has generated new debate about the age of the earth. Some say sea creatures were carried up there by the Great Flood, but others contend that our world is far older than biblical reckoning, and what today are mountains were once beneath the ocean.”
“If that is true, the pyramids may be older than the Bible as well,” I suggested.
“Yes. Changing the scale of time changes everything.” He was running his eye along the limestone, admiring the impressions of shells. “Look, there! We even have a nautilus!”
Talma and I peered over his shoulder. Imbedded in a pyramid block was the cross section of a spiral nautilus shell, one of the most beautiful shapes in nature. From its small corkscrew beginning its chambers grew larger, in pleasing and delicate proportion, as the sea creature grew in an elegant outward spiral. “And what does that make you think of?” Jomard asked.
“Seafood,” Talma said. “I’m hungry.”
Jomard ignored that, staring at the spiral in the rock, transfixed for a reason I didn’t understand. Long minutes ticked by and I dared look out from our perch. A hawk was gliding by at our same elevation. It made me dizzy.
“Jomard?” Talma finally prompted. “You don’t have to watch the fossil. It’s not going to run away.”
As if in reply, the savant suddenly took a rock hammer from his survey bag and tapped at the block’s edges. There was already a crack near the fossil and he worked with this, succeeding in splitting the nautilus specimen loose and cupping it in his hand. “Could it be?” he murmured, turning the elegant creature to see its pattern in light and shadow. He seemed to have forgotten our mission, and us.
“We’ve still a way to go to the top,” I warned, “and the day is getting late.”
“Yes, yes.” He blinked as if waking from a dream. “Let me think about this up there.” He put the shell in his satchel. “Gage, hold the tape. Talma, ready your pencil!”
The summit took another half hour of careful climbing. It was more than 450 feet high, our measuring showed, but we could produce no more than a rough approximation. I looked down. The few French soldiers and Bedouins we could see looked like ants. Fortunately the pyramid’s capstone was gone, so there was a space about the size of a bed on which to stand.
I did feel closer to heaven. There were no competing hills, just flat desert, the winding silver thread of the Nile, and the collar of green on each of its shores. Cairo across the river shimmered with a thousand minarets, and we could hear the wail of the faithful being called to prayer. The battlefield of Imbaba was a dusty arena, dotted with pits where the dead were being tossed. Far to the north, the Mediterranean was invisible over the horizon.
Jomard took out his stone nautilus again. “There is clarity up here, don’t you think? This temple focuses it.” Plopping down, he began to jot some figures.
“And not much else,” Talma said, sitting himself in exaggerated resignation. “Did I mention that I’m hungry?”
But Jomard was lost again in some world of his own, so finally we were quiet for a while, having become accustomed to such meditation by the savants. I felt I could see our planet’s curve, and then scolded myself that it was illusion at this modest height. There did seem a kind of benign focus at the structure’s summit, however, and I actually enjoyed our quiet isolation. Had any other American been up here?
Finally Jomard abruptly rose, picked up a limestone fragment as big as his fist, and hurled it as far as he could. We watched the parabola of its fall, wondering if he could throw far enough to clear the pyramid’s base. He couldn’t, and the stone bounced off the pyramid’s stone blocks below, shattering. Its pieces rattled down.
He looked down the slope for a moment, as if considering his aim. Then he turned to us. “But of course! It’s so obvious. And your eye, Gage, has been the key!”
I perked up. “It has?”
“What a marvel we are standing on! What a culmination of thought, philosophy, and calculation! It was the nautilus that let me see it!”
Talma was rolling his eyes.
“Let you see what?”
“Now, has either of you heard of the Fibonacci sequence of numbers?”
Our silence was answer enough.
“It was brought to Europe about 1200 by Leonardo of Pisa, also known as Fibonacci, after he had studied in Egypt. Its real origin goes much further back than that, to times unknown. Look.” He showed us his paper. On it was written a series of numbers: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55. “Do you see the pattern?”
“I think I tried that one in the lottery,” Talma said. “It lost.”
“No, see how it works?” the savant insisted. “Each number is the sum of the two before it. The next in the sequence, adding 34 and the 55, would be 89.”
“Fascinating,” Talma said.
“Now the amazing thing about this series is that with geometry, you can represent this sequence not as numbers but as a geometric pattern. You do so by drawing squares.” He drew two small squares side by side and put a number 1 inside each. “See, here we have the first two numbers of the sequence. Now we draw a third square alongside the first two, making it as long as they are combined, and label it number 2. Then a square with sides as long as a number 1 square and number 2 square combined, and label it 3. See?” He was sketching quickly. “The side of the new square is the sum of the two squares before it, just as the number in a Fibonacci sequence is the sum of the two numbers before. The squares rapidly get bigger in area.”
Soon he had a picture like this:
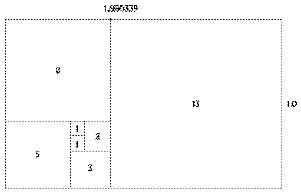
“What does that number at the top, the 1.6 something, mean?” I asked.
“It’s the proportion of the length of the side of each of the squares to the smaller one before it,” Jomard replied. “Notice that the lines of the square labeled 3 have a proportional length with the lines of the squares 2 as, say, the proportion between square 8 and square 13.”
“I don’t understand.”
“See how the line at the top of square 3 is divided into two unequal lengths by its junction with squares 1 and 2?” Jomard said patiently. “That proportion between the length of the short line and the long line is repeated again and again, no matter how big you draw this diagram. The longer line is not 1.5 times the length of the shorter, but 1.618, or what the Greeks and Italians called the golden number, or golden section.”
Both Talma and I straightened slightly. “You mean there’s gold here?”
“No, you cretins.” He shook his head in mock disgust. “Only that the proportions seem perfect when applied to architecture, or to monuments like this pyramid. There’s something about that ratio which is instinctively pleasing to the eye. Cathedrals were built to reflect such divine numbers. Renaissance painters divided their canvases into rectangles and triangles echoing the golden section to achieve harmonious composition. Greek and Roman architects used it in temples and palaces. Now, we must confirm my guess with measurements more precise than those we’ve made today, but my hunch is that this pyramid is sloped precisely to represent this golden number, 1.618.”
“What has the nautilus to do with anything?”
“I’m coming to that. First, imagine a line descending under our feet from the tip of this colossus to its base, straight down to the desert bedrock.”
“I can confirm it is a long line, after that hard climb up,” Talma said.
“More than four hundred and fifty feet,” Jomard agreed. “Now imagine a line from the center of the pyramid to its outside edge.”
“That would be half the width of its base,” I ventured, feeling the same two steps behind that I’d always felt with Benjamin Franklin.
“Precisely!” Jomard cried. “You have an instinct for mathematics, Gage! Now, imagine a line running from that outside edge up the slope of the pyramid to where we are here, completing a right triangle. My theory is that if our line at the pyramid’s base is set as one, such a line up to the peak here would be 1.618—the same harmonious proportion as shown by the squares I’ve drawn!” He looked triumphant.
We looked blank.
“Don’t you see? This pyramid was built to conform to the Fibonacci numbers, the Fibonacci squares, the golden number that artists have always found harmonious. It doesn’t just feel right to us, it
is
right!”
Talma looked across to the other two large pyramids that were our neighbors. “So are they all like that?”
Jomard shook his head. “No. This one is special, I suspect. It is a book, trying to tell us something. It is unique for a reason I don’t yet understand.”
“I’m sorry, Jomard,” the journalist said. “I’m happy for you that you are excited, but the fact that imaginary lines equal 1.6, or whatever you said, seems an even sillier reason to build a pyramid than calling something pointed a hemisphere or building a tomb you won’t be buried in. It seems perfectly possible to me that if any of this is true, your ancient Egyptians were at least as crazy as they were clever.”
